1. 타원곡선의 정의
실수 위에서의 타원곡선은 a와 b가 고정된 실수일 경우에 방정식 y2=x3+ax+b 을 만족하는
(x, y)점들의 집합을 의미한다. 우변인 x3+ax+b가 중근을 갖지 않으면 , 즉 4a3+27b2 ≠ 0 이면
타원곡선은 군을 정의 할 수 있는 대수적 특성을 제공하는 것으로 알려져 있다.
그림 1은 y2=x3-9x-1 인 타원곡선이다. 실수 위에서의 타원곡선 군은 해당 타원곡선 위의 모든
점들과 무한대 점이라고 명명된 특수 점으로 구성되고 여기에 덧셈이 정의된다.
점 P(x1 , y1)과 점 Q(x2, y2)를 더하기 위해서 P와 Q를 잇는 선을 그으면 타원곡선 위의 다른
점 R과 교차한다. 만약 P=Q이면 점 P에 대한 접선을 그으면 된다. 계산한 점 R을 X축에 대칭을
시킨 다른 점 S가 P+Q로 정의된다.
2. 타원곡선 군에서의 덧셈의 특성 ![]() Go
to the Experiment
Go
to the Experiment
1) 무한대 점은 O로 표기하며 타원곡선 위의 임의의 점 P에 대해서 P+O=P가 성립된다.
즉, 무한대 점은 덧셈상의 항등원이 된다.
2) 타원곡선 위의 임의의 점 P에 대해서 P+Q=O를 만족하는 점 Q가 존재하는데 Q=-P로 나타
내며 뺄셈 R-S는 R+(-S)로 정의된다. 점 -P는 점 P의 X축의 대칭점이 되기 때문에 점 P의
좌표가 (x, y)이면 점 -P의 좌표는 (x, -y)이 된다.
3) 타원곡선 위의 임의의 점 P, Q와 R에 대해서 P+(Q+R)=(P+Q)+R이 성립한다.
타원곡선 위의 임의의 점 P와 Q에 대해서 P+Q=Q+P가 성립된다.
그러므로 타원곡선 군은 “가환군”이 된다.
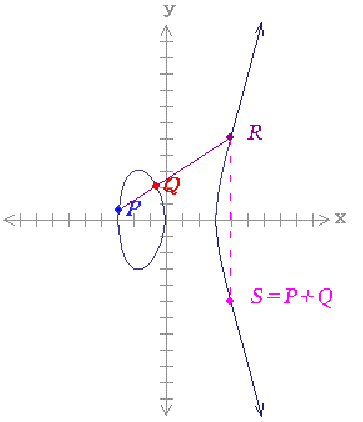
그림 1. 타원곡선 y2=x3-9x-1와 타원곡선 위의 덧셈
3. 타원곡선 위에서의 기하학적 연산
타원곡선 위에서의 기하학적 연산은 그대로 대수적인 연산으로도 설명되어진다.
(x1 , y1), (x2 , y2), (x3 , y3)을 각각 점 P, Q, S=P+Q의 좌표라 한다면, 점 P+Q의 좌표
(x3 , y3)을 통해서 표현 하고자 x1 , x2 , y1 , y2 을 통해서 표현하고자 한다.
R = (x3 , y3)=-S 가 성립한다. y=αx+β 를 점 P와 Q를 지나는 선의 방정식이라 하면,
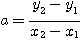 ,
, 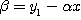
가 된다.
만약, (αx+β)2 = x3+ax+b가 성립한다면 점 P와 Q를 지나는 선 위의 점(x, αx+β)는 타원곡선
위의 점이 된다. 따라서, 3차 방정식 x3 - (αx+β)2 + ax+b의 각각의 근에 대하여 한 개의 교차점
이 존재하게 된다. (x1, αx1+β)와 (x2, αx2+β)는 타원곡선 위의 두 점 P와 Q이기 때문에 이미
우리는 x1, x2가 근임을 알고 있다.
차수가 가장 높은 항의 계수가 1인 다항식에서 그 다항식에 존재하는 모든 근들의 합은 차수가
두 번째로 높은 항의 계수에 ‘-’를 붙은 값과 동일하기 때문에 x1+ x2 + x3 = α2 이 된다.
결국 나머지 근은 x3 = α2 - x1 - x2와 y3 = αx3+β = y1 + α(x3 - x1)이 된다.
그러므로 P+Q를 표현하면,
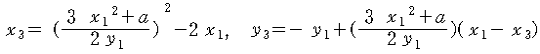
(식 - 1)
P+Q에서 P=Q가 되며 는 점 P에서의 미분 값이 되기 때문에 음함수 미분을 하면 2yy'=3x2 / 2y1
이 되고
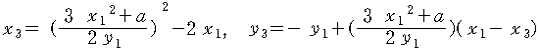
(식 - 2)
[예제 1]
y2 = x3-17x+16 에 의해서 정의되는 타원곡선 위의 두 점 P=(0, -4), Q=(1, 0) 이 주어졌을 때,
P+Q는 다음과 같이 구할 수 있다.
즉, x1=0 , y1 =-4, x2 =1, y2 =0 을 식-1에 대입을 하면 을 얻게 됨으로 P+Q=(15, -56) 이 된다.
실수 계산은 일반적으로 느리며 또한 반올림에 따른 오차로 인하여 정확하지가 않기 때문에
암호 응용에는 적합하지 않다. 따라서, 암호시스템 구축을 위해서는 유한체위에서 정의된 타
원곡선 군이 이용된다.
P가 소수일 때 유한체 GF(P)상에서의 타원곡선은 a,b∈GF(P)의 경우에 방정식 y2 mod p =
x3+ax+b mod p 을 만족하는 (x, y)점들의 집합과 무한대 점 O를 의미한다. 물론 x,y∈GF(P)
이고, 4a3 + 27b ≠0 (mod p) 이면 타원곡선 군이 정의되어진다.
[예제 2]
P=23, a=b=1 인 경우에 GF(P)상에서 타원곡선 y2 = x3 + x +1 이 정의된다.
이 타원곡선 위의 점들은 무한 대 점과 다음의 점들로 구성된다.
(0, 1) (4, 0) (7, 12) (12, 19) (18, 20) (0, 22) (5, 4) (9, 7) (13, 7)
(19, 5) (1, 7) (5, 19) (9, 16) (13, 16) (19, 18) (1, 16) (6, 4) (11, 3)
(17, 3) (3, 10) (6, 19) (11, 20) (17, 20) (3, 13) (7, 11) (12, 4) (18, 3)
유한체 위에서의 타원곡선 군은 유한한 점들의 집합으로 구성되기 때문에 이러한 점들을 어떠
한 방식으로 연결할 지가 명확하지가 않고, 결과적으로 타원곡선 연산을 기하학적으로 표현
하는 것은 어려워진다. 유한체 위에서 정의된 타원곡선 위에 있는 점들간의 덧셈은 실수의 경
우와 동일하게 수행되어 진다. 위의 예제에서 P=(3, 10), Q=(9, 7)의 경우에 P+Q는
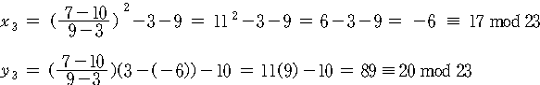
그러므로, P+Q=(17, 20)가 된다.
P위 배수, 즉 2P의 경우에는 P+P와 동일하기 때문에 (식-2)를 적용하여 계산한다.
따라서, 100P를 계산하기 위해서는 2(2(P+2(2(2(P+2P)))))와 같이 할 수 있다. 이것은 효율적인
지수 승 계산에 적용된 알고리즘 “반복 제곱-곱셈”에 대응되는 “반복 2배수-덧셈”이 된다.
4. 타원곡선 이산대수 문제
소수 p에 대해서 GF(p)를 p개의 원소로 구성된 유한체라 하면, 타원곡선 위의 점 P의 위수 t는
tP=O를 만족하는 가장 작은 정수 t로 정의된다. GF(P)상에서 정의된 타원곡선과 점 Q, 그리고
위수가 t인 타원곡선 위의 점 P가 주어졌을 때 Q=xP를 만족하는 정수 x∈[0, t-1]을 구하는 것
을 타원곡선 이산대수 문제라고 한다.
타원곡선 이산대수 문제의 가장 직접적인 해결방법은 Q를 구할 때까지 단순히 P, 2P=P+P,
3P=P+P+P, …를 연속적으로 계산하는 것이지만 t의 값이 매우 클 경우에는 실효성이 게 된다.
지금까지
알려진 가장 효율적인 알고리즘은 Pollard의 rho알고리즘으로서 ![]() 번의
번의
타원곡선 덧셈이 소요된다. Pohlig-Hellman알고리즘 역시 적용이 가능하지만 t가 소수일
경우에는 실효성이 없어지게 된다.
대부분의 학자들에 의해서 타원곡선 이산대수 문제는 소인수 분해나 이산대수 문제보다 훨씬
더 어려운 문제로 인식이 되어진다. 타원곡선 이산대수 문제에 대한 좀 더 적극적인 공격은
Pollard의 rho알고리즘에 기반을 두고 병렬처리를 가능하게 하는 특수목적의 하드웨어를 구
축하는 것이다. 그러나 이러한 공격도 t < 2160 인 경우에는 불가능하게 된다.
현재 타원곡선 암호에 적용 가능한 타원곡선 이산대수의 t값은 단기적으로 150비트, 장기적
으로 180비트 이상이 권고되어지고 있다.
5. 다른 공개키 암호와 비교
RSA공개키 암호나 DSA디지털 서명의 경우에 법 n과 p의 크기가 각각 1024비트 이상이 되어
야 한다. 타원곡선 암호의 경우에는 160비트 이상이 요구된다. 그러므로 타원곡선 암호의 경우
에는 RSA나 DSA보다 짧은 키를 가지고도 높은 수준의 안전성이 보장되기 때문에 실제 구현에
있어서 안전성과 효율성이 모두 뛰어난 암호로 인식되어지고 있다.
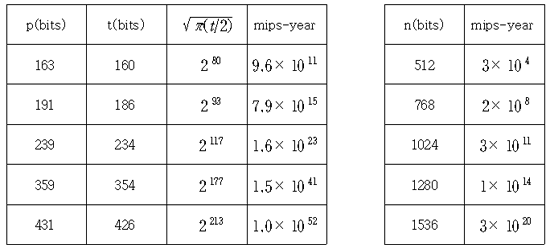
표 1. 타원곡선 이산대수와 소인수 분해에 소요되는 계산량
6. 타원곡선 공개키 암호
이산대수에 기반을 둔 ElGamal 공개키 암호는 타원곡선 이산대수에 기반을 둔 공개키 암호로
전환되어질 수가 있다. 표 2는 두 시스템에서의 암호화 및 복호화 그리고 공개키 및 개인키를
비교하고 있다. 타원곡선 공개키 암호에서는 공개키 G와 Y 그리고 평문 M과 암호문C1과 C2는
모두 타원곡선 위의 점들이다. 두 시스템간의 기본적인 차이점은 ElGamal 공개키 암호에서의
지수승과 곱셈작업이 타원곡선 공개키 암호에서는 각각 배수와 덧셈 작업으로 전환되어진다.

표 2. ElGamal 공개키 암호와 타원곡선 공개키 암호 비교
[예제 3]
p=11, a=1, b=6인 경우에 GF(P)상에서 타원곡선 y2 = x3 + x + 6 주어졌을 때 개인키 x=7, 공개
키 G=(2, 7). Y=7(2, 7)=(7, 2)가 주어진다. 그리고 타원곡선 위의 점들은 다음과 같다.
(2, 4) (2, 7) (3, 5) (3, 6) (5, 2) (5, 9)
(7, 2) (7, 9) (8, 3) (8, 8) (10, 2) (10, 9)
송신자는 임의의 난수 x' = 3을 선정하여 평문 M=(10, 9)을 암호문
C1 = 3(2, 7) = (8, 3), C2= 3(7, 2) + (10, 9) = (10,2)로 전환한다.
평문은 다음과 같이 복호화 된다.
M=(10, 2)-7(8, 3)=(10, 2)-(3, 5)=(10, 2)+(3, 6)=(10, 9)