12.4 삼중적분과 응용
이중 적분의 경우와 마찬가지로 삼중적분 의 값은 반복적분에 의하여 구할 수 있다.
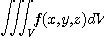
[예제 1] 다음 삼중적분을 계산하여라.
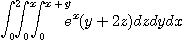
[풀이]  와
와 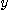 를 상수로 보고
를 상수로 보고
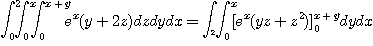

이제  를 상수로 보면,
를 상수로 보면,
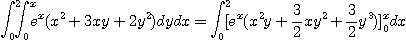
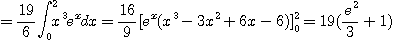
[예제 2] 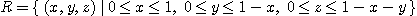 일 때
일 때
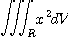
를 구하여라.
[풀이]
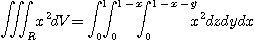
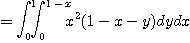
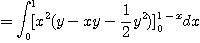
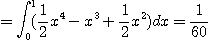
[예제 3] 원주 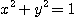 과 평면
과 평면 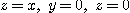 로 둘러싸인 제 1 팔분공간의 영역 의 체적
로 둘러싸인 제 1 팔분공간의 영역 의 체적 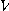 를 구하여라.
를 구하여라.
[풀이]
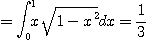
연습문제 12.4
※ 다음 반복적분의 값을 구하여라.
1. 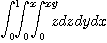
2. 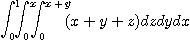
3. 
4. 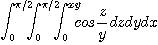
※ 주어진 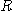 에 대한 삼중적분의 값을 구하여라.
에 대한 삼중적분의 값을 구하여라.
5. 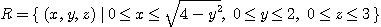
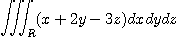
6. 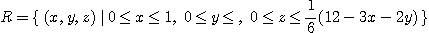
※ 다음 문제에서 주어진 평면 또는 곡면으로 둘러싸인 영역의 체적을 삼중적분으로 구하여라.
7. 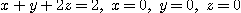
8. 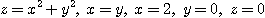
9. 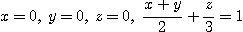
10. 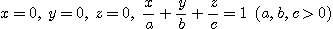
11. 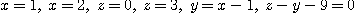
12.5 원기둥좌표와 구면좌표에서의 삼중적분
직각좌표에서와 같이 원기둥좌표(cylindrical coordinates)와 구면좌표(spherical coordinates)에서 주어진 영역으로부터 삼중적분을
정의하기로 하며 이에 대한 계산법도 논하기로 한다.
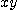 좌표계와
좌표계와  좌표계들이 방정식
좌표계들이 방정식 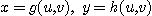 를 만족할 경우,
를 만족할 경우,  와
와  에 대한
에 대한  와
와 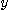 의 야코비안(Jacobian)은
의 야코비안(Jacobian)은
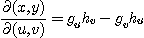
로 정의한다.
[예제 1]  이고
이고 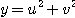 이면,
이면,  와
와  에 대한
에 대한 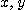 의 야코비안을 구하여라.
의 야코비안을 구하여라.
[풀이]
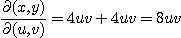
[예제 2] 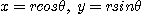 이면
이면 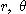 에 대한
에 대한 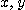 의 야코비안을 구하여라.
의 야코비안을 구하여라.
[풀이]
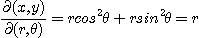
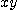 좌표계에서 이중적분
좌표계에서 이중적분
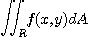
로부터 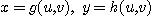 이고 영역
이고 영역 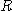 가
가  좌표계에서의 제1영역
좌표계에서의 제1영역
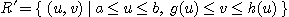
로 변환된다면 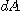 는
는
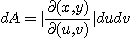
로 치환되어
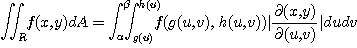
가 성립된다. 이를 치환적분이라 한다. 위와 같은 치환적분을 이용하면 어려운 형태의 적분도 간단히 해결할 수 있다.
[예제 3] 영역 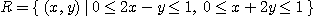 이 주어졌을 때 다음 이중적분을 구하여라.
이 주어졌을 때 다음 이중적분을 구하여라.
[풀이] 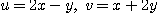 일 때
일 때 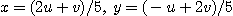 이다. 따라서
이다. 따라서 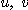 에 대한
에 대한 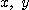 의 야코비안을 계산하면
의 야코비안을 계산하면
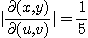
이다. 영역 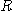 은
은 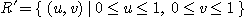 로 변환된다. 그러므로
로 변환된다. 그러므로
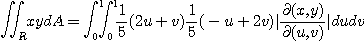
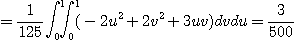
이제부터 삼중적분 특히 원기둥좌표계나 구면좌표계로 쉽게 표현될 수 있는 영역에서의 적분을 치환적분으로 구하는 방법을
알아보기로 하자
직각좌표계와 원기둥좌표계는
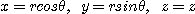
와 같은 관계를 만족하므로 변수 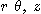 에 관한
에 관한 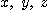 의 야코비안은
의 야코비안은
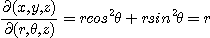
이 된다. 따라서 직각좌표계
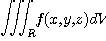
는 원기둥좌표계에서
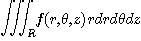
으로 표현되며, 반복적분을 이용하여
삼중적분의 값을 구할 수 있다.
직각좌표계에서의 극좌표, 즉 구면좌표계는
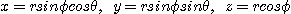
를 만족하므로 변수 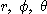 에 관한
에 관한 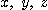 의 야코비안은
의 야코비안은
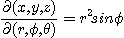
이 된다. 따라서 직각좌표계
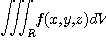
는 구면좌표계에서
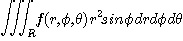
으로 표현되며, 반복적분을 이용하여
삼중적분의 값을 구할 수 있다.
[예제 4] 원통 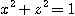 과 평면
과 평면 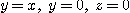 에 의해서 둘러싸인 제 1 팔분원의 입체의 부피는 구하여라.
에 의해서 둘러싸인 제 1 팔분원의 입체의 부피는 구하여라.
[풀이] 다음과 같은 여섯 가지 방법으로 구할 수 있다.
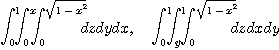
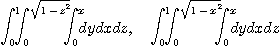
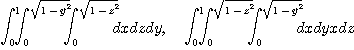
[예제 5] 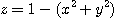 과 평면
과 평면 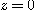 에 의해서 둘러싸인 입체의 부피를 구하여라.
에 의해서 둘러싸인 입체의 부피를 구하여라.
[풀이] 원주좌표에 의해서 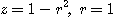 이므로
이므로
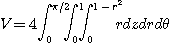
[예제 6] 반경  인 구의 부피
인 구의 부피 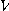 를 구하여라.
를 구하여라.
[풀이]
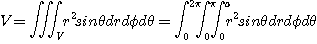
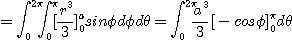
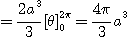
연습문제 12.5
※ 다음 주어진 영역에서의 적분을 구하여라.
1. 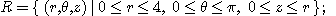
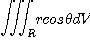
2. 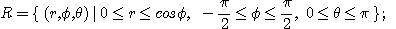
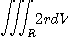
※ 다음 주어진 적분을 원기둥좌표와 구면좌표에서 각각 계산하여라.
3. 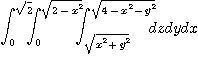
4. 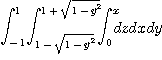
※ 다음 적분을 구면좌표에서 계산하여라.
5. 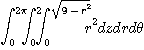
6. 두 원기둥 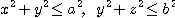 의 교집합으로 이루어진 입체의 부피를 구하여라.
의 교집합으로 이루어진 입체의 부피를 구하여라.
7. 곡면 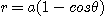 로 둘러싸인 입체의 부피를 구하여라.
로 둘러싸인 입체의 부피를 구하여라.
※ 다음 주어진 입체의 부피를 구하여라.
8. 원기둥 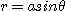 의 내부, 평면
의 내부, 평면 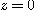 의 위, 구
의 위, 구 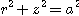 의 내부
의 내부
9. 구 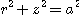 의 내부, 원뿔
의 내부, 원뿔  의 아래
의 아래