제 12 장 다중적분
12.1 이중적분
12.2 이중적분의 응용
12.3 극좌표계의 이중적분
12.4 삼중적분과 응용
12.5 원기둥좌표와 구면좌표에서의 삼중적분
12.1 이중적분
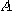 를 둘러싸는 곡선의 아래쪽의 방정식을
를 둘러싸는 곡선의 아래쪽의 방정식을 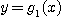 위쪽의 방정식을
위쪽의 방정식을 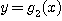 라 하면
라 하면
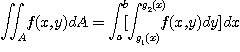
또  를 둘러싸는 곡선의 왼쪽의 방정식을
를 둘러싸는 곡선의 왼쪽의 방정식을 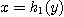 오른쪽의 방정식을
오른쪽의 방정식을 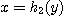 라 하면
라 하면
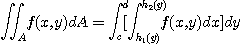
가 된다. 영역 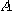 가 직사각형인 경우는 적분순서에 상관 없지만, 직사각형이 아닌 경우에는 적분순서에
유의해야 한다.
가 직사각형인 경우는 적분순서에 상관 없지만, 직사각형이 아닌 경우에는 적분순서에
유의해야 한다.
[예제 1]
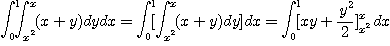
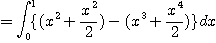
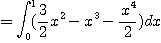
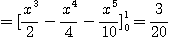
[예제 2]
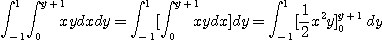
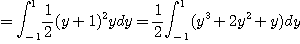
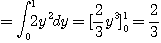
[예제 3] 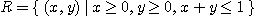 일 때
일 때
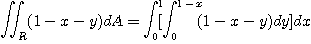
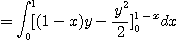
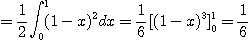
[예제 4] 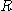 이 포물선
이 포물선 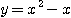 와 직선
와 직선 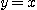 로 둘러싸인 영역일 때 먼저 적분 영역
로 둘러싸인 영역일 때 먼저 적분 영역 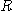 을 구해 보면
을 구해 보면
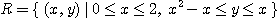
이므로
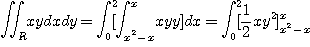
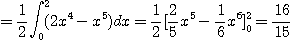
연습문제 12.1
※ 다음 반복적분을 구하여라.
1. 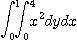 2.
2.
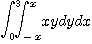
3. 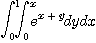
※ 다음 주어진 영역에서의 이중적분을 구하여라.
4. 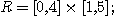
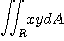
5. 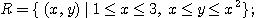
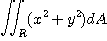
6. 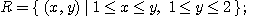
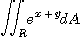
7. 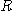 는
는 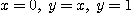 에 둘러싸인 영역;
에 둘러싸인 영역;
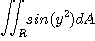
12.2 이중적분의 응용
이중적분
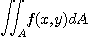
는 영역 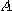 에서
에서 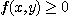 은
은 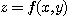 아래의 입체의 부피를 말한다. 그러므로
아래의 입체의 부피를 말한다. 그러므로 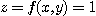 일 경우
일 경우
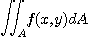
는 영역 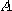 에서 높이가 1인 입체의 부피를 의미한다. 따라서
에서 높이가 1인 입체의 부피를 의미한다. 따라서 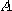 의 넓이와 같다. 이를 이용하여 영역의 넓이를 구할 수
의 넓이와 같다. 이를 이용하여 영역의 넓이를 구할 수
있다.
[예제 1] 두 곡선 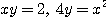 과 직선
과 직선 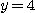 에 의해서 둘러싸인 넓이를 구하라.
에 의해서 둘러싸인 넓이를 구하라.
[풀이] 곡선 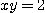 와
와 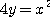 의 교점이
의 교점이 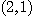 이므로
이므로
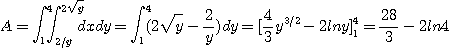
제 7장에서는 회전체의 부피를 계산하는 데 정적분을 이용했다. 이중적분을 이용하여 보다 일반적인 형태의 입체의 부피를 구할 수
있다.
우선 평면의 영역 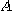 에서 함수
에서 함수  가 양의 값을 갖는다고 하자. 주어진 한 입체의 밑면이 영역
가 양의 값을 갖는다고 하자. 주어진 한 입체의 밑면이 영역 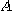 와 일치하고, 이 입체의 윗면이
와 일치하고, 이 입체의 윗면이
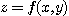 의 그래프와 같은 경우 이 입체를 함수아래의 입체(solid
below )라고 부른다. 만일 함수
의 그래프와 같은 경우 이 입체를 함수아래의 입체(solid
below )라고 부른다. 만일 함수 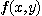 가 영역
가 영역 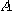 에서 연속이고
에서 연속이고
양의 함수이면 이중적분
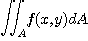
의 값은 함수 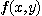 아래 영역의 부피와 같다.
아래 영역의 부피와 같다.
[예제 2] 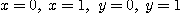 에 둘러싸인 평면 위와 포물선
에 둘러싸인 평면 위와 포물선 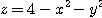 아래에 있는 부피를 구하여라.
아래에 있는 부피를 구하여라.
[풀이]
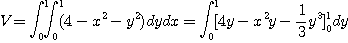
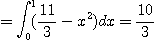
연습문제 12.2
※ 문제 1~5에서 주어진 곡면들에 둘러싸인 입체의 부피를 구하여라.
1. 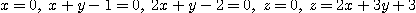
2. 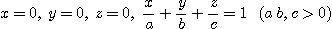
3. 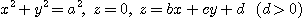
4. 
5. 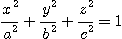
12.3 극좌표계의 이중적분
만일 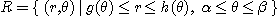 이면 극형식의 이중적분은 아래와 같이 계산된다.
이면 극형식의 이중적분은 아래와 같이 계산된다.
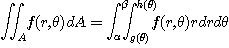
이와 같은 영역 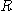 을 제 1극영역(polar region)이라 한다.
을 제 1극영역(polar region)이라 한다.
만일 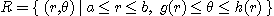 이면
이면

이다. 이렇게 주어진 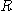 을 제 2극영역이라 한다.
을 제 2극영역이라 한다.
[예제 1] 포물면 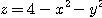 과
과 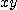 평면으로 둘러싸인 입체의 부피를 극좌표를 이용하여 구하라.
평면으로 둘러싸인 입체의 부피를 극좌표를 이용하여 구하라.
[풀이] 곡면의 방정식은 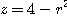 이 되고 이 곡면과
이 되고 이 곡면과 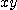 평면의 교선은
평면의 교선은 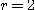 가 된다. 따라서
가 된다. 따라서
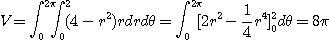
[예제 2] 영역 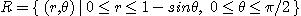 일 때
일 때
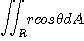
를 계산하여라.
[풀이]
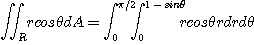
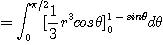
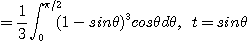
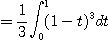
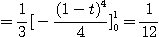
[예제 3] 다음에 주어진 이중적분을 극좌표로 변환하여 구하여라.
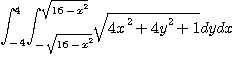
[풀이] 위에서 주어진 이중적분의 영역은
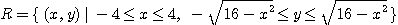
이 되며 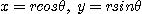 로 치환할 경우
로 치환할 경우
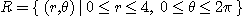
가 된다. 그리고 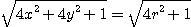 이므로
이므로
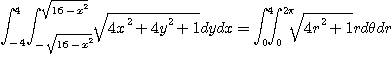

연습문제 12.3
※ 다음에 주어진 곡면과 영역을 각각 상.하면으로 갖는 직원체의 부피를 구하라.
1. 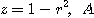 는
는 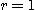 인 제 1 상한의 4분원
인 제 1 상한의 4분원
2. 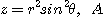 는
는 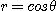 의 제 1상한의 4분원
의 제 1상한의 4분원
※ 극좌표를 써서 다음 입체의 부피를 이중적분으로 구하라.
3. 구면 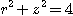 와 원통
와 원통 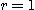 로 둘러싸인 입체
로 둘러싸인 입체
4. 포물면 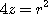 , 평면
, 평면 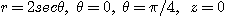 으로 둘러싸인 입체
으로 둘러싸인 입체