11.4 전미분과 응용
이변수 함수 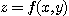 가 주어졌다고 하자. 변수
가 주어졌다고 하자. 변수  가 어떤 값
가 어떤 값  로부터
로부터 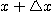 로 변수
로 변수 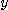 가 어떤 값
가 어떤 값 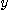 로부터로
로부터로 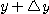 로 변할 때
로 변할 때
주어진 함수의 값은
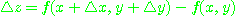
만큼 변한다. 이 양을 주어진 함수의 증분(increment)이라 한다.
[정리 1] 함수 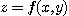 가 주어졌을 때, 만일 세함수
가 주어졌을 때, 만일 세함수
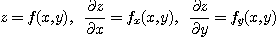
가 모두 점 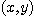 의 근방에서 연속이면
의 근방에서 연속이면
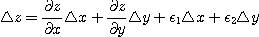
여기서 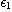 과
과 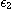 는 다음 성질을 가진 값이다.
는 다음 성질을 가진 값이다.
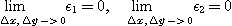
특히 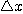 와
와 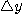 가 충분히 작을 때의
가 충분히 작을 때의 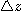 의 근사값으로
의 근사값으로
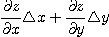
를 취할 수 있다. 이를  의 전미분(total differential)이라 하고, 기호로
의 전미분(total differential)이라 하고, 기호로
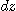 로 나타낸다. 즉,
로 나타낸다. 즉,
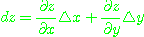
[예제 1] 전미분을 이용하여, 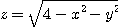 의 점
의 점 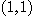 이
이 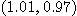 로 움직일 때
로 움직일 때  의 변화의 근사값을 구하여라.
의 변화의 근사값을 구하여라.
[풀이] 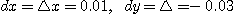
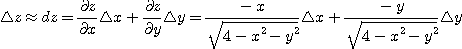
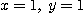 일 때
일 때
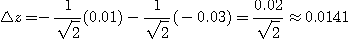
정확한 변화값은 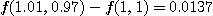 이다.
이다.
[예제 2] 전미분을 이용하여
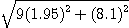
의 근사값을 구하여라.
[풀이] 함수 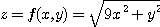 이라 하면,
이라 하면, 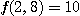 임을 쉽게 구할 수 있다.
임을 쉽게 구할 수 있다.
그래서 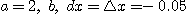 그리고
그리고 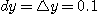 로 잡는다.
로 잡는다.
그러면
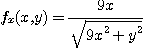 ,
, 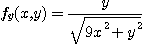
이므로
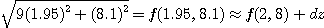
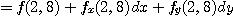
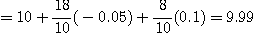
[예제 3] 반경  이
이 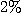 씩 증가하고 높이
씩 증가하고 높이 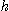 가
가 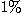 증가하는 원뿔의 변화량을 계산하여라.
증가하는 원뿔의 변화량을 계산하여라.
[풀이] 부피는 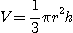 에서
에서 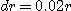 이고
이고 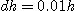 이다. 증가되는 부피는
이다. 증가되는 부피는
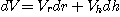
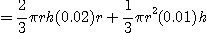
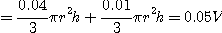
즉 부피는 약 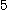 의 증가를 보였다.
의 증가를 보였다.
연습문제 11.4
※ 문제 1~4에서 주어진 함수의 전미분을 구하여라.
1. 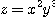 2.
2.
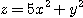
3. 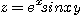 4.
4.
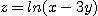
※ 문제 5~6에서 주어진 점에서의 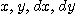 를 얻고 전미분을 사용하여 함수 값을 계산하여라.
를 얻고 전미분을 사용하여 함수 값을 계산하여라.
5. 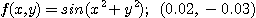
6. 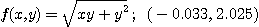
※ 문제 7~8에서 전미분을 이용하여 다음의 근사값을 구하여라.
7. 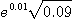
8. 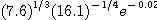
9. 원기둥에서 반경이 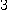 %, 높이 5% 씩 증가할 때 입체의 부피 변화량은?
%, 높이 5% 씩 증가할 때 입체의 부피 변화량은?
10. 타원의 길이가 각 축에서 6과 8이다. 각 축을 0.1씩 늘린다면 그 타원에서
넓이의 변화량은 근사적으로 얼마인가. [ 와
와 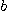 가
가
반축(semiaxes)일 때 넓이는 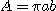 ]
]
11.5 미분가능성과 연쇄법칙
다변수 함수의 미분가능성(differentiability)과 연쇄법칙(chain rule)을 공부하기로 한다.
[정리 1] 미분가능성(differentiability)
이변수 함수 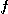 가 점 근방
가 점 근방 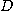 에서 편도함수들을 가지고
에서 편도함수들을 가지고 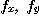 가
가 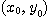 에서 연속이면
에서 연속이면 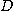 내의 모든 점
내의 모든 점 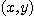 에 대하여
에 대하여
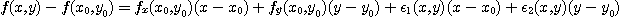
이다. 여기서 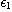 과
과 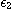 는
는
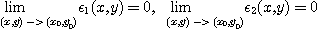
을 만족하는 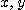 의 함수이다.
의 함수이다.
[정의 1] 미분가능성(differentiability)
점 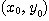 의 근방
의 근방 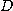 내의 모든 점
내의 모든 점 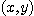 에 대해서
에 대해서
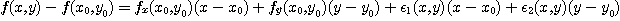
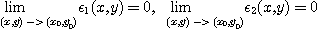
를 만족하는 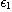 와
와 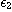 가 존재하면 함수
가 존재하면 함수 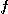 는
는 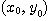 에서 미분가능이라 한다.
에서 미분가능이라 한다.
[정리 2] 이변수 함수 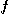 와 그 편도함수
와 그 편도함수 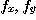 가 연속이면,
가 연속이면, 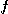 는 그 연속인 범위 안에서 미분 가능하다.
는 그 연속인 범위 안에서 미분 가능하다.
[정리 3] 이변수 함수 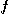 가
가 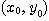 에서 미분 가능하면
에서 미분 가능하면 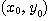 에서 연속이다.
에서 연속이다.
[정의 2] 연쇄법칙
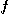 는
는  와
와  의 이변수 함수로서 미분가능하고
의 이변수 함수로서 미분가능하고  와
와  는 모두
는 모두  와
와 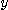 의 이변수 함수로서 미분 가능하다고 하면
의 이변수 함수로서 미분 가능하다고 하면  와
와 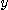 에 관한
에 관한 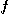 의
의
편도함수가 존재하여 다음의 조건을 만족한다.
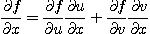
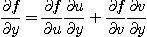
[예제 2] 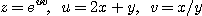 일 때
일 때 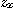 와
와 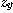 를 구하여라.
를 구하여라.
[풀이] 연쇄법칙을 이용하면
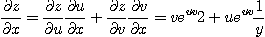
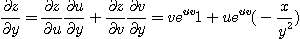
[예제 3] 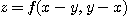 일 때
일 때
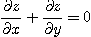
임을 보여라.
[풀이] 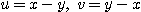 라 두면
라 두면 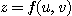 이고 연쇄법칙을 이용하면
이고 연쇄법칙을 이용하면
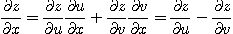
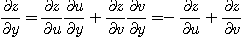
이 되므로 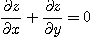 이다.
이다.
[예제 4] 어떤 가스의 압력이 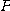 , 체적이
, 체적이 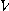 , 온도를
, 온도를 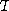 라고 하고
라고 하고 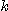 를 상수라 할 때 식
를 상수라 할 때 식 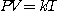 가 성립한다고 한다. 1제곱 인치에
가 성립한다고 한다. 1제곱 인치에
작용하는 압력이 시간(초)당 0.05 파운드씩 증가하며 1세제곱 인치당 부피의 감소율이 시간(초)당 0.25 세제곱 인치라고 한다.
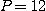 파운드,
파운드, 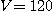 세제곱 인치일 때 시간당 온도의 변화율은 얼마인가?
세제곱 인치일 때 시간당 온도의 변화율은 얼마인가?
[풀이] 준식으로부터 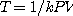 를 얻는다. 따라서
를 얻는다. 따라서
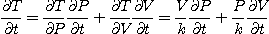
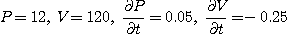
이므로
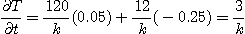
따라서 온도는 시간(초)당 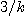 씩 증가한다.
씩 증가한다.
연습문제 11.5
※ 문제 1~4에서 주어진 함수에서 연쇄법칙을 이용하여 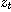 를 구하여라.
를 구하여라.
1. 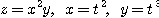 2.
2.
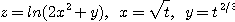
3. 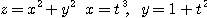 4.
4.
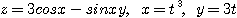
※ 문제 5~9에서 주어진 함수에서 와 를 구하여라.
5. 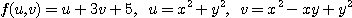
6. 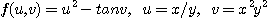
7. 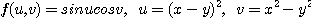
8. 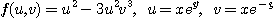
9. 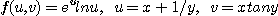
※ 문제 10~12에서 연쇄법칙을 써서 다음을 구하여라.
10. 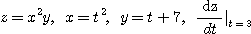
11. 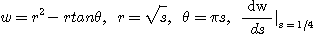
12. 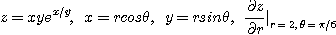
※ 문제 13~16에서 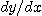 를 구하여라.
를 구하여라.
13. 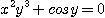 14.
14.
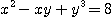
15. 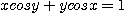 16.
16.
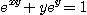
17. 삼각형의 밑변이 시간당 2cm씩 증가하고 높이는 시간당 0.5 cm씩 감소한다고 한다. 밑변이 20cm이고 높이가 12cm일 때
삼각형의 넓이는 시간당 얼마씩 변화하는가?
18. 어떤 전기회로에서 배터리가 방전됨에 따라서, 전압 V 가 서서히 감소하고, 저항 R 는 저항기가 뜨거워짐에 따라서 서서히
증가한다고 한다. 옴의 법칙 V=IR 를 사용해서 R=400, I=0.08, dV/dt=-0.01V/s, dR/dt=0.03/s 일 때 전류 I의 변화율을 구하여라.
19. 직원뿔의 높이가 시간당 25cm 씩 증가하고 밑변의 반지름은 시간당 50cm씩 감소한다고 한다. 어느 시점에서 밑변의 반지름과
높이가 모두 1m 이었다고 한다. 이 시점에서의 시간당 부피의 변화율을 구하여라.
20. 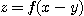 일 때
일 때
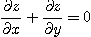
임을 보여라.
21. 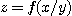 일 때
일 때
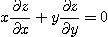
임을 보여라.
11.6 방향미분계수와 경사도
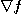 를
를 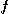 의 그래디언트(gradient)라 하며
의 그래디언트(gradient)라 하며
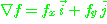
여기에서 기호 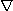 를 델(del)이라 읽고 다음과 같이 표시한다.
를 델(del)이라 읽고 다음과 같이 표시한다.

이 때
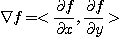
이고, 점 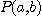 에서
에서 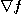 의 값은
의 값은
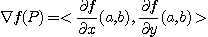
이다.
[예제 1] 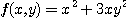 일 때
일 때 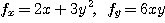 이므로
이므로 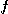 의 그래디언트는
의 그래디언트는
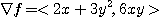
따라서
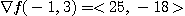
[정의 1] 방향도함수(directional derivative)
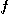 를 이변수 함수라 하고
를 이변수 함수라 하고 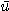 를 단위벡터라하자.
를 단위벡터라하자. 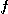 의
의 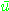 방향의 방향도함수(directional derivative) 는 극한이 존재할 때 다음과
같이
방향의 방향도함수(directional derivative) 는 극한이 존재할 때 다음과
같이
정의한다.
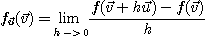
[정리 1] 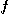 를 이변수 함수라 하고
를 이변수 함수라 하고 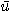 를 단위벡터라 한다.
를 단위벡터라 한다. 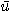 방향의
방향의 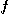 의 방향도함수는 다음과 같다.
의 방향도함수는 다음과 같다.
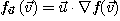
[예제 2] 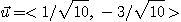 이고
이고 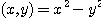 일 때 점
일 때 점 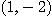 에서의
에서의 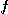 의 방향도함수를 구하여라.
의 방향도함수를 구하여라.
[풀이] 주어진 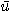 는 단위벡터이므로
는 단위벡터이므로 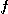 의 그래디언트를 구하면
의 그래디언트를 구하면
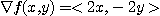
따라서 방향도함수는
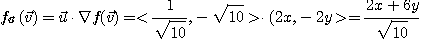
그러므로
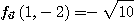
[정리 2] 이변수 함수 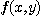 가 미분 가능하다고 하자
가 미분 가능하다고 하자
1) 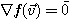 이면 모든
이면 모든 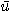 에 대하여도
에 대하여도 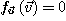 이다.
이다.
2) 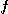 의 최대증가의 방향은
의 최대증가의 방향은 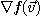 로 주어진다.
로 주어진다.
3) 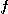 의 최소증가의 방향은
의 최소증가의 방향은 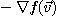 로 주어진다.
로 주어진다.
[예제 3] 점(1,-2)에서 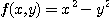 의 최대, 최소 변화율을 각각 구하여라.
의 최대, 최소 변화율을 각각 구하여라.
[풀이] 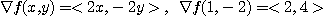
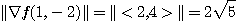
따라서 최대변화율은 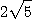 이고 최소 변화율은
이고 최소 변화율은 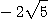 이다.
이다.
[예제 4] 어떤 금속판 표면의 온도는 등고선 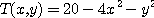 으로 분포되어 있다. 점
으로 분포되어 있다. 점 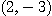 에서 온도가 가장 급격히
증가
에서 온도가 가장 급격히
증가
하는 방향과 비율을 구하여라.
[풀이] 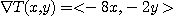
최대증가의 방향은 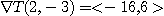 이므로 비율은
이므로 비율은
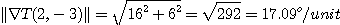
이다.
연습문제 11.6
※ 문제 1~4에서 주어진 점에서 각 함수의 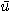 방향으로의 방향도함수를 구하여라.
방향으로의 방향도함수를 구하여라.
1. 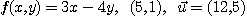
2. 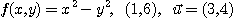
3. 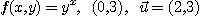
4. 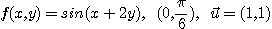
※ 문제 5~6에서 다음 함수들의 주어진 점과 각 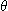 에 의하여 주어진 방향에서 방향도함수를
구하여라.
에 의하여 주어진 방향에서 방향도함수를
구하여라.
5. 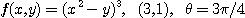
6. 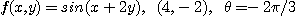
※ 문제 7~10에서 다음 함수들의 주어진 각 점에서 주어진 벡터 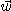 방향의 방향도함수를
구하여라.
방향의 방향도함수를
구하여라.
7. 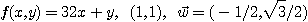
8. 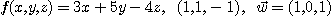
9. 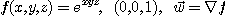
10. 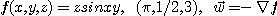
※ 문제 11~12에서 다음 함수들의 주어진 각 점에서 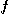 의 값의 최대변화가 일어나는
방향벡터와
의 값의 최대변화가 일어나는
방향벡터와 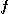 의 최대변화율을 구하여라.
의 최대변화율을 구하여라.
11.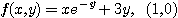
12. 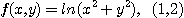
13.철판 위의 한 점 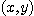 에서의 온도가
에서의 온도가 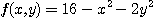 이라 할 때 점
이라 할 때 점 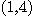 에서
에서 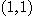 방향과 최대 온도 방향의 온도
변화율을
방향과 최대 온도 방향의 온도
변화율을
각각 구하여라.