제 11 장 편도함수
11.1 이 변수 함수
11.2 극한과 연속
11.3 편도함수
11.4 미분가능성과 연쇄법칙
11.5 전미분
11.6 접평면과 법선
11.7 최대, 최소
11.1 다변수함수
[정의 1] 이변수 함수
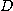 를 실수의 쌍
를 실수의 쌍 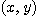 의 집합이라 하자.
의 집합이라 하자. 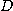 의 각 원소
의 각 원소 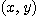 에 실수
에 실수 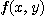 를 하나씩 대응시키는 규칙
를 하나씩 대응시키는 규칙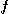 를 이변수 함수(function of
를 이변수 함수(function of
two variables)라고 한다. 이 때 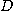 를 정의역(domain)이라 하며
를 정의역(domain)이라 하며 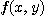 를
를 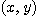 의
의 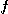 에 의한 상(image)이라 한다. 그리고
에 의한 상(image)이라 한다. 그리고 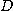 를
를
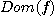 로 나타내기도 한다.
로 나타내기도 한다. 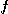 의 치역은 각
의 치역은 각 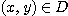 에 대한 값
에 대한 값 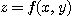 들의 집합이다. 또 점
들의 집합이다. 또 점  들의 집합을
들의 집합을  의 그래프
의 그래프
(graph)라 한다.
일변수 함수와 같이 이변수 함수도 식으로 표시될 수 있으며 정의역을 분명하게 언급하지 않는 경우도 있다. 이런 경우에는 주어진
함수식을 성립하도록 하는 점 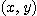 전체의 집합을 정의역으로 간주한다. 일변수 함수의 그래프가 평면 위의 곡선이듯이
이변수
전체의 집합을 정의역으로 간주한다. 일변수 함수의 그래프가 평면 위의 곡선이듯이
이변수
함수의 그래프는 공간 속의 곡면(surface)임을 알 수 있다.
[예제 1] 함수 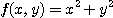 에서
에서 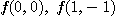 의 값을 각각 구하고, 또
의 값을 각각 구하고, 또 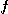 의 정의역과 치역을 찾아보아라.
의 정의역과 치역을 찾아보아라.
[풀이] 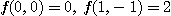 이다.
이다.
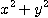 은
은  와
와 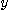 의 모든 값에 대하여 값을 가지므로
의 모든 값에 대하여 값을 가지므로 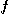 의 정의역은 평면 전체이다.
의 정의역은 평면 전체이다.
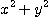 의 값은
의 값은 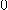 이상이므로
이상이므로 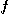 의 치역은
의 치역은 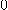 이상의 실수 전체이다.
이상의 실수 전체이다.
[예제 2] 다음 함수의 정의역과 치역을 구하여라.
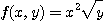
[풀이] 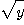 로부터
로부터 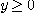 이다. 따라서 정의역은
이다. 따라서 정의역은
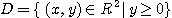
이고 또 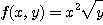 이므로
이므로 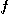 의 치역은
의 치역은 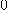 이상의 실수 전체이다.
이상의 실수 전체이다.
[정의 2] 다변수 함수
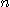 을 양의 정수라 하고
을 양의 정수라 하고 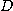 를
를 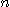 개의 순서쌍
개의 순서쌍 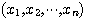 들의 집합이라 하자.
들의 집합이라 하자. 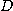 의 각 원소
의 각 원소  에 실수
에 실수 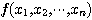 를
를
하나씩 대응시키는 규칙 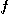 를
를  변수 함수(function of
변수 함수(function of  variables)라고 한다. 이 때
variables)라고 한다. 이 때 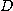 를 정의역이라 하며 함수값
를 정의역이라 하며 함수값 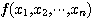 들의
들의
집합을 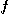 의 치역이라 한다.
의 치역이라 한다.
연습문제 11.1
※ 문제 1~6에서 각 함수의 정의역을 정하여라.
1. 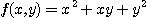 2.
2.
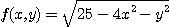
3. 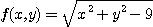 4.
4.
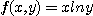
5. 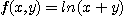 6.
6.
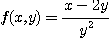
11.2 극한과 연속
일변수 함수 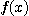 에서
에서 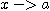 라는 뜻은 변수
라는 뜻은 변수  가
가  의 왼쪽이나 오른쪽에서
의 왼쪽이나 오른쪽에서  에 가까워진다는 뜻이다.
에 가까워진다는 뜻이다.
그러나 이변수 함수의 경우 평면 위의 점 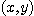 가 점
가 점 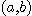 에 가까워지는 경로는 무수히 많다. 그래서
에 가까워지는 경로는 무수히 많다. 그래서 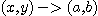 라는 뜻은
라는 뜻은 
에서 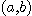 에 이르는 거리가 그 접근하는 길에 상관없이
에 이르는 거리가 그 접근하는 길에 상관없이 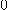 에 가까워지는 것을 말한다. 또한 일변수 함수의 경우
에 가까워지는 것을 말한다. 또한 일변수 함수의 경우 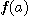 가 정의되지
가 정의되지
않아도 함수의 극한을 정의할 수 있다. 먼저 평면 위의 한 점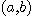 를 중심으로 하고 반지름
를 중심으로 하고 반지름  인 원 내부 점들의 집합을
인 원 내부 점들의 집합을 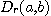 로
로
표시하기로 한다. 즉
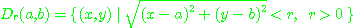
이때 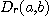 를 점
를 점 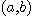 의
의 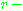 근방(neighborhood)이라 한다.
근방(neighborhood)이라 한다.
[정의 1] 이변수 함수의 극한
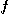 가 점
가 점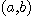 의 어떤 근방
의 어떤 근방 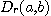 에서 정의된 이변수 함수라 하자. 임의로 주어진
에서 정의된 이변수 함수라 하자. 임의로 주어진 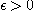 에 대해서
에 대해서

이 유한 확정값 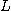 에 대하여 반드시 성립하면
에 대하여 반드시 성립하면
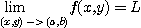
이라 쓰고 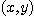 가
가 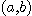 로 수렴할 때 함수
로 수렴할 때 함수 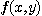 의 극한(limit)은
의 극한(limit)은 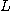 이라고 한다.
이라고 한다.
주의 : 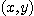 가
가 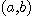 로 가까워 지는 경로에 관계없이
로 가까워 지는 경로에 관계없이 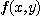 가 같은 값으로 가까워 질 때 극한은 존재한다. 이것은 우리가 일변수
가 같은 값으로 가까워 질 때 극한은 존재한다. 이것은 우리가 일변수
함수에서 우극한과 좌극한이 같을 때 극한이 존재하는 것과 같은 이치이다.
[예제 1] 함수 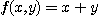 가
가 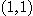 에서 극한 2를 가짐을
에서 극한 2를 가짐을 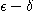 방법으로 증명하여라.
방법으로 증명하여라.
[풀이] 임의의 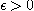 에 대하여
에 대하여
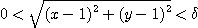
일 때  가 형성하게 되는
가 형성하게 되는 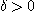 을 찾아내면 된다.
을 찾아내면 된다.
그런데
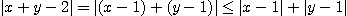
이므로
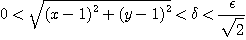
일 때
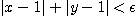
이 성립하게 된다.
연습문제 11.2
1. 함수
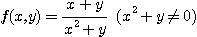
에 대하여,
(a) 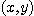 가 직선
가 직선 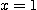 에 따라서
에 따라서  일 때의
일 때의
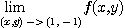
를 구하여라.
(b) 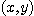 가 직선
가 직선  에 따라서
에 따라서  일 때의
일 때의
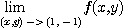
를 구하여라.
2.
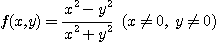
일 때 직선 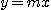 를 따라서
를 따라서 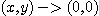 일 때
일 때
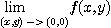
는 존재하는가?
11.3 편도함수
일변수 함수의 도함수를 구하기 위하여 적용하던 몇 가지 원리들을 이변수 함수에,
나아가서 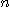 변수 함수에 적용함으로써 편도함수의
변수 함수에 적용함으로써 편도함수의
개념을 알게 된다.
[정의 1] 편도함수(partial derivative)
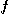 를
를  와
와 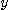 의 이변수 함수라 하자. 이 때
의 이변수 함수라 하자. 이 때 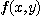 의
의  에 관한 편도함수(partial derivative)
에 관한 편도함수(partial derivative) 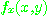 와
와 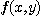 의
의 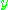 에 관한 편도함수를
에 관한 편도함수를
각각 극한값이 존재할 경우에 다음과 같이 정의한다.
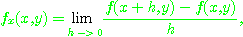
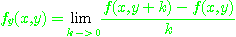
[예제 1] 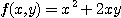 일 때 편도함수 정의를 이용하여
일 때 편도함수 정의를 이용하여 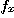 를 구하여라.
를 구하여라.
[풀이]
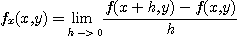
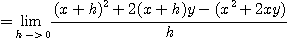
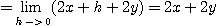
편도함수의 정의에서 알 수 있듯이 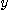 를 상수로 생각하고
를 상수로 생각하고 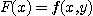 라 놓으면
라 놓으면
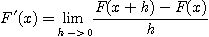
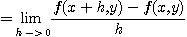
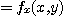
임을 알 수 있다. 즉 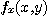 를 구할 때에는
를 구할 때에는 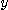 를 상수로 간주하고
를 상수로 간주하고  에 관해서 미분하면 된다. 이 방법은
에 관해서 미분하면 된다. 이 방법은 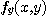 를 계산할 때에도
를 계산할 때에도
같다.
함수가 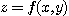 로 주어졌으면 편도함수
로 주어졌으면 편도함수 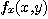 대신에
대신에 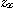 로
로 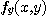 대신에
대신에 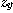 로 표시하기도 한다. 즉
로 표시하기도 한다. 즉
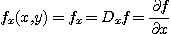
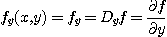
점 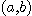 에서의
에서의 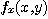 의 함수값을
의 함수값을 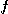 의
의  에 관한 편미분계수(partral derivative)라 하고
다음과 같이 표시하기로 한다.
에 관한 편미분계수(partral derivative)라 하고
다음과 같이 표시하기로 한다.
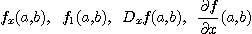
[예제 2] 이변수 함수 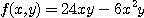 의 편도함수들과 점
의 편도함수들과 점 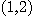 에서의 편미분계수들을 구하여라.
에서의 편미분계수들을 구하여라.
[풀이] 먼저 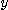 를 상수로 간주하고
를 상수로 간주하고 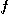 를
를  에 관하여 미분하면
에 관하여 미분하면
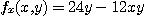
이고 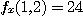 이다. 또
이다. 또  를 상수로 보고
를 상수로 보고 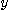 에 관하여 미분하면
에 관하여 미분하면
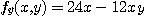
이고 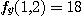 이다.
이다.
다음 식이 성립함은 쉽게 알 수 있다.
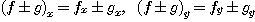
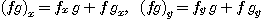
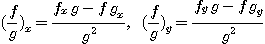
[예제 3]
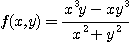
의 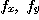 를 구하여라.
를 구하여라.
[풀이] 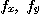 는
는 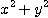 이
이 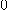 이 아닌 점, 즉
이 아닌 점, 즉 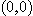 을 제외한 모든 점에서 정의되고 위 공식에 의하여
을 제외한 모든 점에서 정의되고 위 공식에 의하여
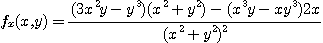
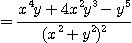
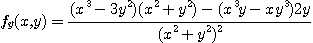

이변수 함수 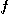 의 편도함수
의 편도함수 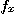 와
와  는 이변수함수이고 이 함수들이 다시
는 이변수함수이고 이 함수들이 다시  와
와 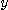 에 관해서 편미분가능하다면 다음과 같은
에 관해서 편미분가능하다면 다음과 같은 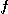 의
의
제 2계편도함수(second partial derivative)들을 얻을 수 있다. 같은 방법으로 고계도함수를 정의할 수 있다.
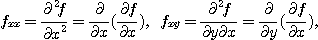
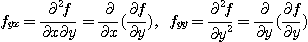
[예제 4] 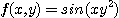 의 제2계편도함수를 구하여라.
의 제2계편도함수를 구하여라.
[풀이] 우선 제1계편도함수들을 구하면
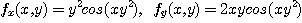
이므로 이것들을 다시 편미분하면
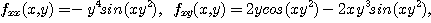
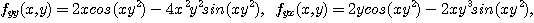
[정리 1] Schwarz 정리
이변수 함수 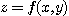 가
가 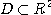 에서 연속인 편도함수
에서 연속인 편도함수 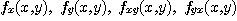 를 가질 때 이 영역에서
를 가질 때 이 영역에서
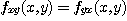
이다.
연습문제 11.3
※ 문제 1~4에서 주어진 각 함수에서 1계 및 2계 편도함수를 모두 구하여라.
1. 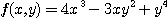 2.
2.
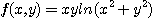
3. 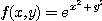 4.
4.
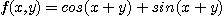
5. 전류의 흐름에서 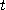 를 시간,
를 시간, 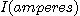 를 세기,
를 세기, 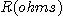 을 저항이라 할 때 발생하는 열
을 저항이라 할 때 발생하는 열 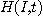 는 다음과 같다고 하자.
는 다음과 같다고 하자.
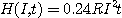 .
.
이때 시간에 대한 열량의 변화율을 구하여라.(단위는 칼로리임)
6. 다음의 각 함수가 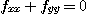 을 만족함을 보여라.
을 만족함을 보여라.
(1) 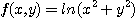
(2) 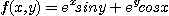
7. 원기둥의 부피 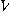 는
는 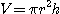 (
( 은 반지름,
은 반지름, 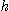 는 높이)로 주어진다. 다음 각 물음에 답하여라.
는 높이)로 주어진다. 다음 각 물음에 답하여라.
(1) 높이가 일정할 때 반지름  에 관한 부피의 변화율을 구하여라.
에 관한 부피의 변화율을 구하여라.
(2) 반지름이 일정할 때 높이 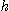 에 관한 부피의 변화율을 구하여라.
에 관한 부피의 변화율을 구하여라.
(3) 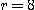 이고
이고 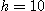 일 때 높이에 관한 부피의 변화율을 구하여라.
일 때 높이에 관한 부피의 변화율을 구하여라.
8. 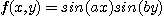 가 다음의 파동방정식(wave equation)을 만족함을 보여라.
가 다음의 파동방정식(wave equation)을 만족함을 보여라.