10.4 벡터함수와 곡률
지금까지 공부한 함수는 실수를 값으로 갖는 함수였다. 이제 공간에서 곡선이나 질점의 운동을 설명하는 데 필요한 값이 벡터인
함수를 공부하기로 하자. 일반적으로, 함수는 정의역이 각 원소에 치역의 한 원소를 대응시키는 규칙에 따라 정의되었다.
벡터를 값으로 갖는 함수 또는 벡터함수(vector-valued function)는 단순히 그 정의역이 실수의 집합이고, 그 치역이 벡터의 집합인
함수이다. 우리가 관심을 가지는 벡터함수  는
그 값이 삼차원 벡터인 것이다. 이것은
는
그 값이 삼차원 벡터인 것이다. 이것은  의 정의역에 있는 모든 실수
의 정의역에 있는 모든 실수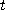 에 대하여
에 대하여 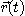
가
존재한다는 것을 의미하며, 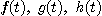 가 벡터함수의 성분들이라면 이것을
가 벡터함수의 성분들이라면 이것을
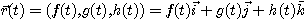
로 쓴다. 벡터함수의 대부분의 응용에서 변수 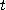 는 시간을 나타내기 때문에, 독립변수를
표시하는 데 이것을 사용한다.
는 시간을 나타내기 때문에, 독립변수를
표시하는 데 이것을 사용한다.
[정의 1] 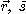 가 벡터함수이고
가 벡터함수이고 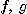 가 실수값을 갖는 함수 일 때, 벡터함수
가 실수값을 갖는 함수 일 때, 벡터함수
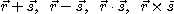
는 각각 다음과 같이 정의된다.
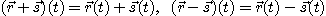
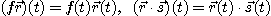
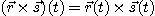
벡터함수의 극한은 다음과 같이 그 성분함수들의 극한을 택함으로써 정의된다.
[정의 2] 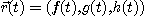 일 때, 각 성분함수의 극한이 존재하면
일 때, 각 성분함수의 극한이 존재하면
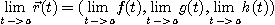
이다.
[예제 1] 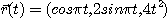 일 때,
일 때, 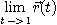 를 구하여라.
를 구하여라.
[풀이] 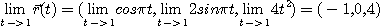
[정의 3] 벡터함수  는
는

일 때, 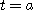 에서 연속이라고 한다. 즉
에서 연속이라고 한다. 즉
 가
가  에서 연속일 필요충분조건은 그 성분함수
에서 연속일 필요충분조건은 그 성분함수 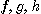 가
가
 에서 연속인 것을 알 수 있다.
에서 연속인 것을 알 수 있다.
지금부터는 벡터함수의 미분과 적분에 대해서 공부하기로 하자.
[정의 4] 벡터함수  의 정의역 내에 속하는 점
의 정의역 내에 속하는 점 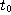 에 대하여, 극한값
에 대하여, 극한값
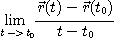
이 존재하면 벡터함수  는
는 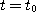 에서 미분 가능하다고 하고, 이 극한값을
에서 미분 가능하다고 하고, 이 극한값을 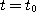 에서의 벡터함수
에서의 벡터함수  의
미분계수(differential
의
미분계수(differential
coefficient)라 하며 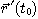 로 나타낸다.
로 나타낸다.
[정리 1] 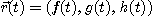 벡터함수가
벡터함수가 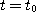 에서 미분가능하기 위한 필요충분조건은 함수
에서 미분가능하기 위한 필요충분조건은 함수 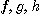 모두가
모두가 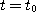 에서 미분
에서 미분
가능한 것이다. 이때
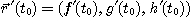
이다.
[정의 5] 벡터함수 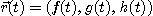 가
가 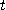 에서 미분가능할 때
에서 미분가능할 때
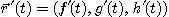
를  의 도함수라고 한다. 마찬가지로
의 도함수라고 한다. 마찬가지로  의 2계도함수
의 2계도함수 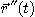 와
와 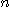 계도함수
계도함수 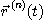 를 정의할 수 있다.
를 정의할 수 있다.
벡터함수의 도함수의 경우 미분법에서 다룬 도함수에 관한 법칙이 거의 대부분 성립한다.
[정리 2] 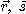 를 미분가능한 벡터함수,
를 미분가능한 벡터함수, 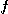 를 미분가능한 실수함수라 하면,
를 미분가능한 실수함수라 하면,
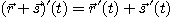
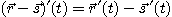
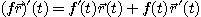
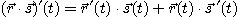
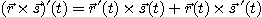
[예제 3]  (상수)이면,
(상수)이면, 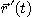 는 모든
는 모든 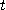 에 대하여
에 대하여 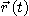 와 직교임을 보여라.
와 직교임을 보여라.
[풀이] 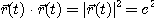
이고, 위의 미분공식에 의하여
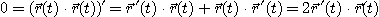
따라서 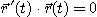 이고, 이것은
이고, 이것은 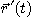 가
가 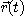 에 직교임을 말해 준다.
에 직교임을 말해 준다.
벡터함수의 미분에 관한 개념의 중요한 응용은 움직이는 물체의 속도, 가속도등을 구하는 것이다. 즉
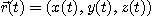
에서 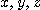 를 각각 시간
를 각각 시간 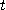 의 함수로서 운동하는 물체의 각 방향에서의 위치를 나타낸다고
하고, 또 이 함수가 각각 2계도함수를
의 함수로서 운동하는 물체의 각 방향에서의 위치를 나타낸다고
하고, 또 이 함수가 각각 2계도함수를
갖는다고 하면
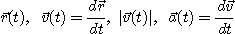
는 각각 이 물체의 시각 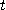 에서의 위치, 속도, 속력, 가속도가 된다. 또
에서의 위치, 속도, 속력, 가속도가 된다. 또 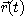 가
가 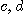 를 포함하는
어떤 구간 위에서 미분가능하면
를 포함하는
어떤 구간 위에서 미분가능하면
시각 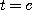 에서
에서 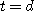 까지 이 물체가 움직인 거리
까지 이 물체가 움직인 거리  는
는
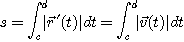
로 주어지며, 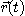 가 일반벡터함수일 때에
가 일반벡터함수일 때에  는 호의 길이가 된다.
는 호의 길이가 된다.
[예제 4] 매개방정식
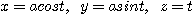
로 주어지는 곡선을 원나선(circular helix)이라 한다. 이 원나선의 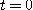 부터
부터 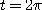 까지의
호의 길이를 구하여라.
까지의
호의 길이를 구하여라.
[풀이]
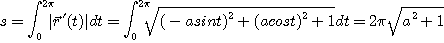
[정의 6] 함수 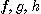 가 구간
가 구간 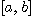 에서 연속이라고 하자. 이때 벡터함수
에서 연속이라고 하자. 이때 벡터함수 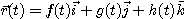
의 부정적분와 정적분는 각각 다음과 같이 정의한다.
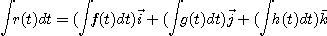
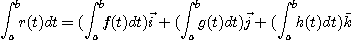
구간  위에서 미분가능한 벡터함수
위에서 미분가능한 벡터함수 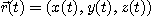 의 변수
의 변수 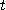 가
가  에서
에서 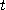 까지 변할 때 위치벡터
까지 변할 때 위치벡터 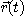 의 종점이
그리는
의 종점이
그리는
호의길이는
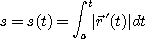
로 주어짐을 알았다.
지금부터는 공간곡선의 형태를 조사하는 데 매우 유용한 곡률, 단위접선벡터, 주법선벡터, 종법선벡터 등에 대하여 공부하기로 하자.
구간 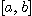 에서 2계도함수를 갖는 벡터함수
에서 2계도함수를 갖는 벡터함수 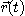 의 종점
의 종점 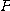 가 그리는 곡선을
가 그리는 곡선을  라고 하자. 이때
라고 하자. 이때
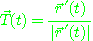
를 점 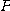 에서의 곡선
에서의 곡선 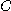 의 단위접선벡터(unit tangent vector) 라고 한다. 단위접선벡터의
방향은 곡선 위의 점
의 단위접선벡터(unit tangent vector) 라고 한다. 단위접선벡터의
방향은 곡선 위의 점 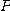 에서의 접선방향
에서의 접선방향
이고, 길이는 항상 1이다. 즉 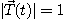 이다. 벡터
이다. 벡터 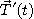 는 단위접선벡터
는 단위접선벡터 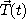 에
수직이며 곡선의 안쪽을 향한다. 이 벡터
에
수직이며 곡선의 안쪽을 향한다. 이 벡터 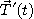 와
와
같은 방향을 갖는 단위벡터, 즉
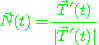
를 점 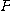 에서의 곡선
에서의 곡선 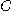 의 주법선벡터(pricipal normal vector)라고 하며, 단위접선벡터
의 주법선벡터(pricipal normal vector)라고 하며, 단위접선벡터
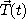 와
주법선벡터
와
주법선벡터 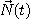 의 시점이 둘 다
의 시점이 둘 다 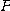
라고 생각할 때 이들 벡터에 의하여 만들어지는 평면을
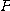 에서의 곡선
에서의 곡선 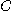 에 대한 접촉평면(osculatingplane)이라 한다.
에 대한 접촉평면(osculatingplane)이라 한다.
또한 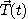 와
와 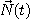 에 동시에 수직인
벡터
에 동시에 수직인
벡터
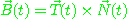
를 점에 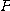 에서의 곡선
에서의 곡선 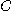 의 종법선벡터(binormal vector)라고 하는데
의 종법선벡터(binormal vector)라고 하는데 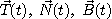 는 서로 직교하는
우수계(right hand system)
는 서로 직교하는
우수계(right hand system)
를 이루며 이들은 공간곡선을 살피는 데 유용하게 이용된다.
이제 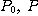 를 각각
를 각각 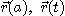 의 종점이라 하고
의 종점이라 하고 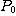 부터
부터 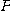 까지의 곡선의 길이를
까지의 곡선의 길이를  라고 하자. 즉
라고 하자. 즉
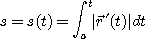
이때  에 관한 단위접선벡터
에 관한 단위접선벡터 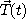 의 순간변화율
의 순간변화율
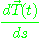
를 점 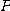 에서의 곡선
에서의 곡선 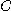 의 곡률벡터(curvature vector)라고 한다. 한편, 합성함수의
미분법을 이용하면 곡률벡터는
의 곡률벡터(curvature vector)라고 한다. 한편, 합성함수의
미분법을 이용하면 곡률벡터는
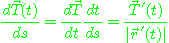
로 표현된다.
[정의 7] 벡터함수 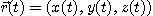 의 종점이 그리는 곡선위의 점
의 종점이 그리는 곡선위의 점 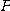 에서의 곡률벡터의 크기를 점
에서의 곡률벡터의 크기를 점 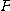 에서의 곡률(curvature)
에서의 곡률(curvature)
이라고
하고 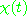 로 나타낸다. 즉
로 나타낸다. 즉
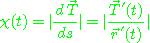
또 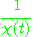 를 곡률반지름(radius of curvature)이라고 한다.
를 곡률반지름(radius of curvature)이라고 한다.
[예제 5] 원나선위 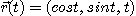 의 임의의 점에서의 곡률을 구하여라.
의 임의의 점에서의 곡률을 구하여라.
[풀이]
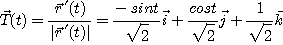
따라서
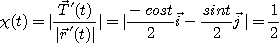
이므로 원나선의 곡률은 모든점에서 일정하다.
공간곡선의 곡률을 구하는데 정의를 직접 사용하는 것보다 다음 결과를 이용하는 것이 편리할 때가 많다.
[정리 3] 벡터함수 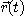 가 2계도함수를 가지면 다음이 성립한다.
가 2계도함수를 가지면 다음이 성립한다.
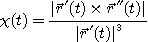
[예제 6]
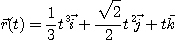
의 곡률을 구하여라.
[풀이] 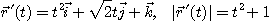
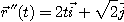
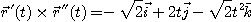
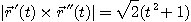
그러므로
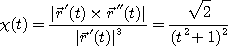
이다.
연습문제 10.5
※ 매개변수 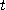 의 주어진 값에 의한 점에서 단위접선벡터를 구하여라.
의 주어진 값에 의한 점에서 단위접선벡터를 구하여라.
1. 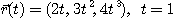
2. 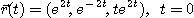
3. 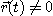 일 때,
일 때,
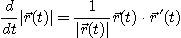
임을 보여라.
※ 주어진 곡선의 길이를 구하여라.
4. 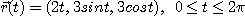
5. 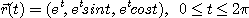
6. 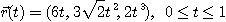
7. 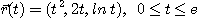
※ 다음에 주어진 곡선 위의 임의점에서의 단위접선벡터, 주법선벡터 및 곡률을 구하여라.
8. 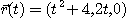
9. 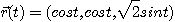
10. 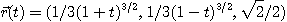
11. 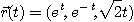
12. 원나선 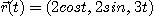 위의 임의점에서의 종법선벡터를 구하여라.
위의 임의점에서의 종법선벡터를 구하여라.