제 9 장 수열과 무한급수
9.1 수열
9.2 무한급수
9.3 수렴판정법
9.4 멱급수
9.5 함수의 멱급수 전개
9.1 수열
집합 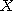 안에서 수열(sequence)이란 자연수
안에서 수열(sequence)이란 자연수 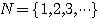 위에서 집합
위에서 집합  에 포함되는 치역으로의 함수를 말한다. 일반적으로
에 포함되는 치역으로의 함수를 말한다. 일반적으로
수열은 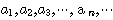 으로 나타내기도 하고 간단히
으로 나타내기도 하고 간단히
 ,
, 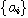
로 나타낸다.
[정의 1] 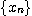 은 실수열이고
은 실수열이고 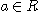 이라고 할 때, 임의의 양수(아무리 작은 수일지라도)
이라고 할 때, 임의의 양수(아무리 작은 수일지라도)  에 대하여 적당한 자연수
에 대하여 적당한 자연수 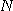 이 존재하여
이 존재하여
모든 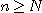
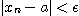
를 만족 할 때 수열 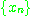 은
은  로 수렴한다(converges to a)라고 하며
로 수렴한다(converges to a)라고 하며  는 수열
는 수열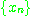 의 극한(limit)이라고 하고
의 극한(limit)이라고 하고
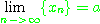
로 나타낸다. 수렴하지 않는 수열은 발산한다(diverges)고 한다.
[예제 1] 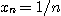 이라고 하자. 그러면
이라고 하자. 그러면 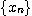 은
은 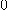 으로 수렴한다.
으로 수렴한다.
[풀이] 임의의 양수  이 주어질 때,
이 주어질 때, 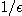 은 존재하고 양수이다. 아르키메데스 정리에 의하여 적당한 자연수
은 존재하고 양수이다. 아르키메데스 정리에 의하여 적당한 자연수 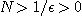 이 존재한다.
이 존재한다.
그러므로 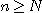 에 대하여 다음을 만족시킬 수 있다.
에 대하여 다음을 만족시킬 수 있다.
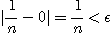 .
.
[예제 2] 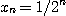 이라고 하자. 그러면 수열
이라고 하자. 그러면 수열 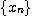 은
은 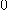 으로 수렴한다.
으로 수렴한다.
[정리 1] 압축정리
수열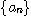 은
은 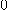 으로 수렴하고, 모든
으로 수렴하고, 모든 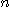 에 대하여
에 대하여 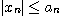 이 성립할 때, 수열
이 성립할 때, 수열 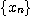 은
은 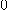 으로 수렴한다.
으로 수렴한다.
[따름 정리] 수열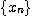 이
이  로 수렴한다는 것은 수열
로 수렴한다는 것은 수열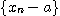 가
가 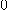 으로 수렴하는 것과 동치이다.
으로 수렴하는 것과 동치이다.
[예제 3]
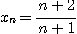
이라고 하자. 그러면 수열 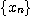 은 1로 수렴한다.
은 1로 수렴한다.
[풀이] 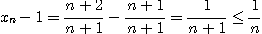
이므로 압축정리에 의하여 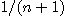 은
은 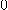 으로 수렴한다. 그러므로 따름 정리에 의하여
으로 수렴한다. 그러므로 따름 정리에 의하여 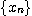 은
은 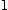 로 수렴한다.
로 수렴한다.
만약 수열 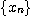 이
이  로 수렴할 때, 이 수열이 동시에 다른 수로 수렴한다는 것은 합당하지 않은 것처럼
보인다.
로 수렴할 때, 이 수열이 동시에 다른 수로 수렴한다는 것은 합당하지 않은 것처럼
보인다.
그래서 다음의 정리가 중요하다.
[정리 2] 유일성
수렴하는 수열의 극한은 유일하다.
다음의 중요한 내용은 수렴하는 수열의 합, 곱 그리고 나누기의 극한은 그 수열의 극한의 합, 곱 그리고 나누기와 같다는 것이다.
[정리 3] 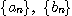 이 수렴하는 수열이고
이 수렴하는 수열이고 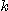 가 상수일 때, 다음결과들이 성립한다.
가 상수일 때, 다음결과들이 성립한다.
(1) 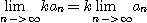
(2) 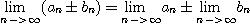
(3) 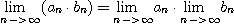
(4) 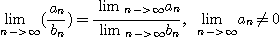
[예제 3]

을 구하여라.
[풀이]
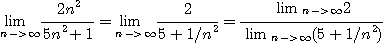
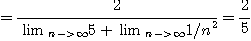
[정의 2] 어떤 상수 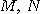 이 있을 때, 모든
이 있을 때, 모든 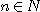 에 대하여 각각
에 대하여 각각
(1) 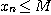 이면,
이면,  을 수열
을 수열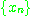 의 상계(upper bound)라 하며,
의 상계(upper bound)라 하며, 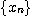 은 상계 에 의해 위로 유계되었다(bounded above)고
한다.
은 상계 에 의해 위로 유계되었다(bounded above)고
한다.
(2) 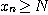 이면,
이면, 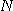 을 수열의 하계(lower bound)라 하며,
을 수열의 하계(lower bound)라 하며, 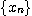 은 하계 에 의해 아래로 유계되었다(bounded below)고
한다
은 하계 에 의해 아래로 유계되었다(bounded below)고
한다
(3)  이면, 수열
이면, 수열 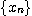 은 유계(bounded)라고 한다.
은 유계(bounded)라고 한다.
[예제 4] 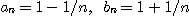 일 때
일 때 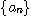 은 1에 의해 위로 유계된 수열이고
은 1에 의해 위로 유계된 수열이고 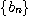 은 1에 의해 아래로 유계된 수열이다.
은 1에 의해 아래로 유계된 수열이다.
[정리 4] 수열 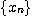 이 수렴하면
이 수렴하면 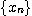 은 유계이다.
은 유계이다.
[정의 3] 모든 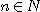 에 대하여
에 대하여 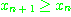 이면 수열은 증가한다(increasing)고 하며,
이면 수열은 증가한다(increasing)고 하며,
만약 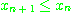 이면 감소한다(deceasing)고 한다. 수열이
증가수열이거나 감소수열 둘 중에 하나일 때
이면 감소한다(deceasing)고 한다. 수열이
증가수열이거나 감소수열 둘 중에 하나일 때
단조수열(monotone sequence)이라고 한다.
[예제 4]  은 감소수열이고
은 감소수열이고 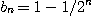 은 증가수열이다.
은 증가수열이다.
다음으로 수열의 수렴, 발산을 판별하는 유용한 정리를 소개하기로 하자.
[정리 5] 단조수열정리
수열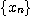 이 단조수열이고 유계이면 수열
이 단조수열이고 유계이면 수열 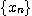 은 수렴한다
은 수렴한다
단조수열정리의 증명은 생략하나, 이 정리는 실수의 중요한 성질인 완비성(completeness property)과 동치이다..
[예제 5] 다음과 같이 정의된 수열이 수렴함을 보여라.
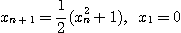
[풀이] 1. 증가수열임을 보이자.
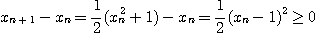
2. 유계임을 보이자.
수학적
귀납법에 의해 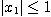 이고 만약
이고 만약 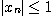 이면
이면
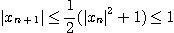
그러므로 단조수열정리에 의해 수열 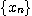 은 수렴한다.
은 수렴한다.
연습문제 9.1
※ 다음 수열의 일반항을 구하고, 수렴성을 조사하여라.
1. 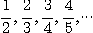
2. 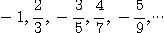
3. 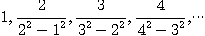
4. 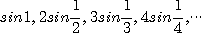
※ 다음 수열의 수렴성을 조사하여라. 또, 수렴하는 수열은 그 극한을 구하여라.
5. 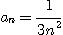 6.
6.
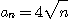
7. 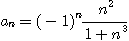 8.
8.
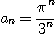
9. 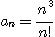 10.
10.
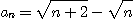
※ 주어진 수열이 증가하는지, 감소하는지 아니면 단조수열인지를 조사하여라.
11. 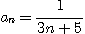 12.
12.

13. 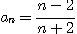 14.
14.
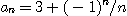
15. 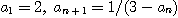 으로 주어진 수열
으로 주어진 수열 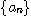 이
이 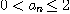 이고 감소함을 보여라.
이고 감소함을 보여라.
또 이 수열이 수렴함을 보이고 그 극한을 구하여라.
16. 다음 수열의 극한을 구하여라.
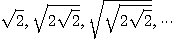
17.
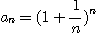
일 때, 다음 물음에 답하여라.
(a) 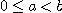 이면
이면
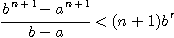
임을 보여라.
(b) 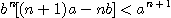
임을 보여라.
(c) (b)에서 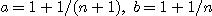 인 경우를 이용하여
인 경우를 이용하여 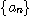 이 증가함을 보여라.
이 증가함을 보여라.
(d) (b)에서 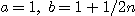 인 경우를 이용하여
인 경우를 이용하여 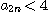 임을 보여라
임을 보여라
(e) (c) 와 (d) 를 이용하여 모든 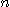 에 대하여
에 대하여 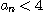 임을 보여라.
임을 보여라.
(f) 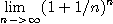 이 존재함을 보여라.
이 존재함을 보여라.
9.2 무한급수
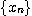 이 실수열이라 할 때 우리는 무한개의 실수들의 합을 구하고 덧셈을 무한번 시행하는
방법은 생각할 수 있으나 실행은
이 실수열이라 할 때 우리는 무한개의 실수들의 합을 구하고 덧셈을 무한번 시행하는
방법은 생각할 수 있으나 실행은
불가능하다. 그래서 다음과 같은 극한 개념을 사용할 것이다.
[정의 1] 주어진 수열 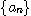 에 대하여
에 대하여
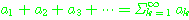
을 무한급수(infinite series) 또는 급수(series)라고 하며,
처음  항까지의 합
항까지의 합

을 이 급수의 부분합(partial sum)이라 한다.
부분합들의 수열 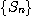 의
의
극한
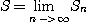
이 존재하면 급수
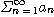
은 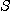 에 수렴한다라 하고
에 수렴한다라 하고 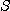 를 이 급수의 합(sum) 이라고 하며
를 이 급수의 합(sum) 이라고 하며
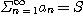
로
나타낸다. 수렴하지 않는 급수는 발산한다(diverges)고 한다.
일반적으로 급수가 수렴하는지 혹은 발산하는지를 결정하는데 필요한 부분 합을 정확히 계산하는 것이 불가능한 경우가 있다.
하지만 다음의 무한등비급수는 쉽게 부분 합을 구할 수 있다.
[예제 1] 기하급수
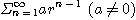
에서  이면 수렴하고 그 합은
이면 수렴하고 그 합은
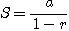
이고 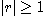 이면 발산한다.
이면 발산한다.
[풀이] 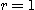 이면 부분합
이면 부분합 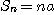 이므로 발산한다.
이므로 발산한다.
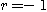 이면
이면
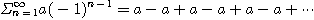
이므로 역시 발산한다.
 라 가정하자. 이 때의 부분합
라 가정하자. 이 때의 부분합 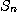 은
은
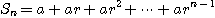
이고 양변에  을 곱하면
을 곱하면
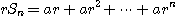
이므로
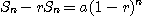
따라서
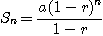
 이면
이면
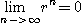
이므로
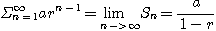
만일 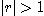 이면 은
이면 은
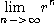
존재하지 않으므로 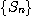 은 발산한다.
은 발산한다.
[예제 2] 다음의 등비급수의 합을 구하여라.
(1) 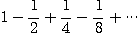
(2) 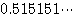
[풀이] (1) 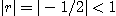 이므로 이 무한급수는 수렴하고
이므로 이 무한급수는 수렴하고
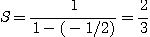
(2) 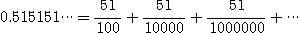
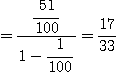
[정리 1] 급수
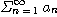
이 수렴하면
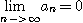
이다.
[증명] 정의에 의하여 급수
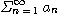
이 수렴하면
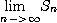
이 존재하고
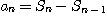
이다. 따라서
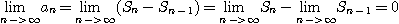
정리 1의 동치조건으로 무한 급수의 발산을 증명하는데 유용한 조건은 다음과 같이 쉽게 알 수 있다.
[따름 정리]
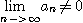
이면 급수
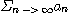
은 발산한다.
[예제 3] 무한급수
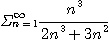
이 발산함을 보여라.
[풀이]
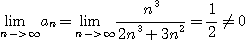
따라서 따름 정리에 의하여 급수는 발산한다.
정리 1에서 수렴하는 급수의 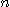 항은
항은 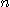 이 커짐에 따라
이 커짐에 따라 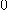 에 접근함을 알 수 있다. 그러나 그 역은 성립하지 않는다.
에 접근함을 알 수 있다. 그러나 그 역은 성립하지 않는다.
즉
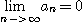
이라는 조건은 급수 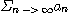 이 수렴할 필요조건은 되지만 충분조건은 되지 않는다.
이 수렴할 필요조건은 되지만 충분조건은 되지 않는다.
다음예제에서
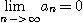
이지만 발산하는 급수의 예를 보자.
[예제 4] 조화급수(harmonic series)
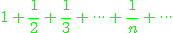
이 발산함을 보여라.
[풀이]
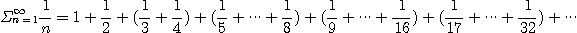
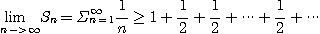
따라서
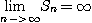
이므로 발산한다.
[정리 2] 선형성(linearity)
급수
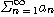 ,
, 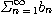
이 수렴하고  가 상수이면
가 상수이면
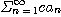 ,
, 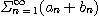
역시 수렴한다.
(1) 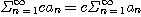
(2) 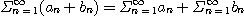
연습문제 9.2
※ 다음 수열의 수렴, 발산을 조사하고, 수렴하는 경우에는 그 합을 구하여라.
1. 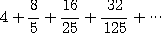 2.
2.
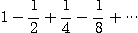
3. 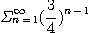 4.
4.
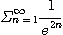
5. 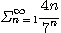 6.
6.
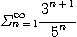
7. 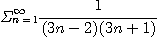 8.
8.
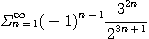
9. 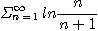 10.
10.
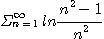
※ 다음 각 소수를 무한급수로 표현하고 그 합을 구하여라.
11. 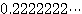 12.
12.
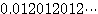
9.3 수렴판정법
이번 절에서는 급수의 수렴성을 판별하는 여러 가지 방법들을 소개할 것이다.
특히 각 항이 양수인 급수는 비교적 쉽게 수렴성을 알 수가 있다.
[정의 1] 각 항이 양수인 급수를 양항급수(positive terms series)라고 한다.
[정리 1] 양항급수
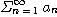
이 있을 때 그 부분합 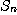 의 수열이 위로 유계이면
의 수열이 위로 유계이면
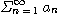
은 수렴한다.
[증명] 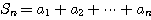 에서
에서 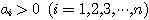 이므로
이므로 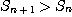 이다.
이다.
단조수열정리에 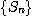 의하여 이 위로 유계이면
의하여 이 위로 유계이면
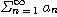
이 수렴한다.
[예제 1] 급수
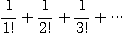
이 수렴함을 보여라.
[풀이] 정리 1에 의해서 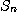 이 위로 유계임을 보이면 된다.
이 위로 유계임을 보이면 된다.
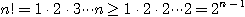
이므로
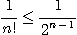
이다.
따라서
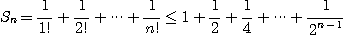
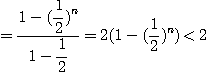
그러므로 급수는 수렴한다.
[정리 2] 적분판정법 (Integral Test)
급수
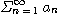
의 각 항은 양수이고 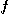 가
가 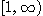 위에서 정의되고 감소함수이며 연속이라고 하자.
위에서 정의되고 감소함수이며 연속이라고 하자.
만일 모든 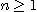 에 대하여
에 대하여 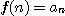 이면
이면
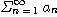
이 수렴하기 위한 필요충분조건은 특이적분
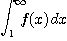
가 수렴하는 것이다.
[예제 2] 조화급수
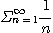
이 발산함을 보여라.
[풀이]
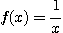
은 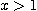 에서 감소함수이고 연속이다. 모든
에서 감소함수이고 연속이다. 모든 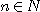 에 대하여
에 대하여

이라 하면
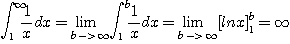
따라서
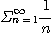
은 발산한다.
[정의 2] p-급수
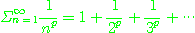
의 형태로 된 급수를 p-급수(p-series)라고 한다.
[예제 3] p-급수
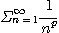
은 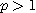 이면 수렴하고
이면 수렴하고 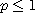 이면 발산한다.
이면 발산한다.
[풀이] 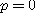 이면
이면

은 발산한다.
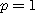 이면
이면
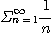
역시 발산한다.
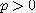 이면 구간
이면 구간 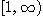 위에서 함수
위에서 함수
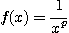
은 연속이며 감소함수이다. 따라서 적분판정법에 의하여
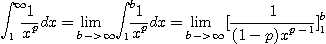
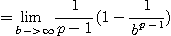

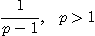
따라서  이면 p-급수는 수렴하고
이면 p-급수는 수렴하고 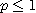 이면 발산한다.
이면 발산한다.
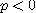 이면
이면
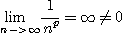
이므로
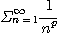
은 발산한다.
적분판정법 이외에도 양항급수의 몇 가지 판정법을 소개하겠다. 그리고 기하급수와 p-급수에서 수렴 및 발산에 대해 얻은 결과들을
다른 급수의 수렴성을 판정하는데 이용하자.
[정리 3] 비교판정법(Comparison Test)
모든 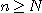 에 대하여
에 대하여 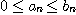 일 때
일 때
(1)
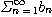
이 수렴하면
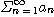
도 수렴한다.
(2)
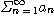
이 발산하면
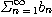
도 발산한다.
[예제 4] 급수
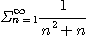
이 수렴함을 보여라.
[풀이] 모든 자연수 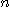 에 대하여
에 대하여
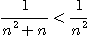
이고
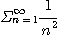
이 수렴하므로 비교판정법에 의하여
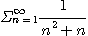
은 수렴한다.
[예제 5] 급수
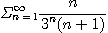
이 수렴함을 보여라.
[풀이] 모든 자연수 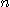 에 대하여
에 대하여
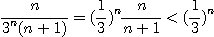
이고,
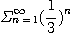
이 수렴하므로 비교판정법에 의하여
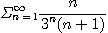
은 수렴한다.
[정리 4] 극한비교판정법(Limit Comparison Test)
모든 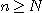 에 대하여
에 대하여 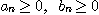 이고 만일 극한
이고 만일 극한
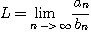
이면 다음이 성립한다.
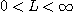 이면
이면
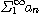 ,
, 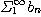
은 동시에 수렴하거나 동시에 발산한다.
[예제 6] 다음 급수
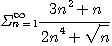
의 수렴성을 조사하라.
[풀이]
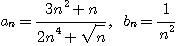
이라면
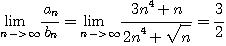
한편,
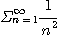
은 수렴하므로 극한비교판정법에 의하여
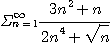
은 수렴한다.
[예제 7] 다음 급수
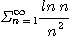
의 수렴성을 조사하라.
[풀이]
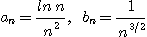
일 때 p-급수 판정법에 의하여
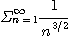
은 수렴한다.
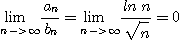
이므로 극한비교판정법에 의하여
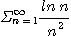
은 수렴한다.
[정의 3] 급수의 항이 양, 음이 교대로 나타날 때, 즉 모든 자연수
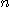 에 대하여
에 대하여 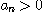 일 때
일 때
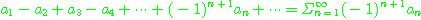
인 형태의 급수를 교대급수(altenating series)라고 한다.
예를 들면,
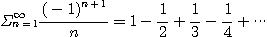
는 교대급수이다.
[정리 5] 교대급수판정법(Alternating Series Test)
만일
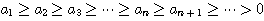
이고

이면 교대급수
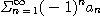
은 수렴한다.
이 경우 급수의 합이 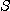 이고
이고  항까지의
부분합이
항까지의
부분합이 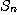 이면
이면 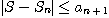 이다.
이다.
[예제 8] 교대조화급수
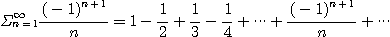
의 수렴성을 조사하라.
[풀이]
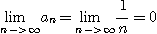
이고
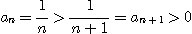
이므로 교대급수 판정법에 의하여 이 급수는 수렴한다.
[정의 4] 급수

에서
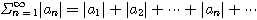
이 수렴할 때
급수
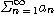
는 절대수렴(absolutely convergent)한다고 한다.
[정리 6] 급수
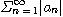
이 수렴하면
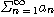
도 수렴한다.
[예제 9] 급수
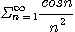
의 수렴성을 조사하라.
[풀이]
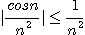
이며
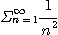
은 p-급수판정법에 의하여수렴하므로 비교판정법에 의하여
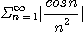
이 수렴한다.
따라서 정리 6에 의하여
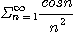
은 수렴한다.
[정의 5] 수렴은 하나 절대수렴은 하지 않는 급수를 조건부수렴(conditionally convergent)한다고 한다.
[예제 10]
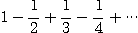
가 조건부 수렴함을 보여라.
[풀이] 교대급수판정법에 의하여 수렴하고 p-급수 판정법에 의하여 절대수렴하지 않는다.
[정리 7] 비판정법(Ratio Test)
급수
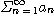
의 각 항이 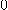 이 아니라고 가정하자.
이 아니라고 가정하자.
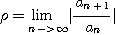
일 때
(1) 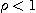 이면 이 급수는 절대수렴하고
이면 이 급수는 절대수렴하고
(2) 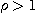 이면 이 급수는 발산하며
이면 이 급수는 발산하며
(3) 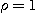 이면 이 급수의 수렴성을 판정할 수 없다.
이면 이 급수의 수렴성을 판정할 수 없다.
[예제 11] 다음 급수의 수렴성을 조사하라.
(1) 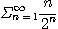 (2)
(2)
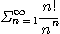
[풀이]
(1)
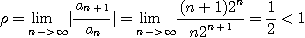
따라서 절대수렴한다.
(2) 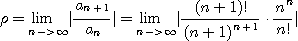

따라서 절대수렴한다.
[정리 8] n-승근 판정법(n-th Root Test)
급수
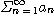
에서
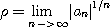
일 때
(1) 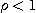 이면 이 급수는 절대수렴하고
이면 이 급수는 절대수렴하고
(2) 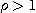 이면 이 급수는 발산하며
이면 이 급수는 발산하며
(3) 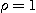 이면 이 급수의 수렴성을 판정할 수 없다.
이면 이 급수의 수렴성을 판정할 수 없다.
[예제 12] 다음 급수의 수렴성을 조사하라.
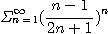
[풀이] n-승근 판정법에 따라

따라서 절대수렴한다.
연습문제 9.3
※ 다음급수의 수렴, 발산을 조사하여라.
1. 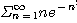 2.
2.
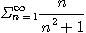
3. 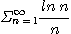
4. 다음 급수가 수렴하기 위한 p의 값을 구하여라.
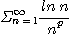
※ 다음급수의 수렴, 발산을 조사하여라.
5. 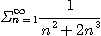 6.
6.
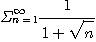
7.  8.
8.
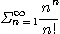
9. 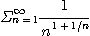 10.
10.
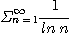
※ 다음급수의 수렴, 발산을 조사하여라.
11. 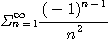 12.
12.
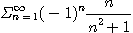
13. 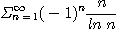 14.
14.
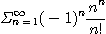
※ 다음 급수가 절대수렴하는지, 조건수렴하는지 아니면 발산하는지를 조사하여라.
15. 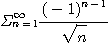 16.
16.
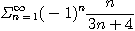
17. 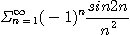 18.
18.
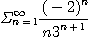
19. 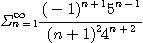 20.
20.