1.4.3 Bessel 방정식과 Legendre 방정식

      이제 응용수학, 수리물리학 또는 기타 여러 공학 분야에서 중요한 역할을 하는 대표적인 2개의 미분방정식에 대해 알아보자.

현이나 막의 진동, 원통형 도체에서의 전류의 전도 또는 원통안에서 열의 흐름 등에서 나타나는 미분방정식

을   차의 Bessel 미분방정식(Bessel's equation)이라 한다.

여기서 로 가정한다.

그리고 구상도체 및 열분포의 경계값 문제등에서 유용하게 사용되는 미분방정식

을 차의 Legendre 미분방정식 (Legendre's equation)이라 한다.

여기서 는 음이 아닌 정수의 경우만을 생각한다.

1.4.3.1 Bessel 방정식의 급수해

 Bessel 방정식

(4.30)                                                         

의 급수해를 구해보자.

는 식 (4.30)의 정칙특이점이므로 을 해라고 가정할 수 있다. 따라서

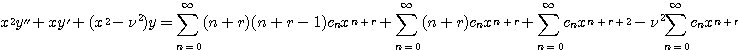
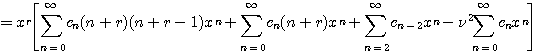
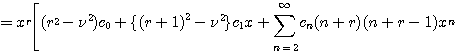
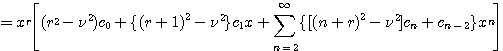
가 된다. 따라서

을 얻는다. 그러므로 결정근과 순환관계식은 다음과 같다.

(4.31)                           

(I)   인 경우

    식 (4.31)에서 순환관계식

을 얻는다. 따라서

이 됨을 알 수 있다. 여기서 를 특정한 값 즉   로 택하는 것이 표준관례이다.

여기서 는 Gamma함수로서

로 정의되고 이 적분은    즉 에서 수렴한다.

      순환관계식 가 성립함은 부분적분을 해보면 쉽게 알 수 있다.

이므로

이 성립하고 이 양의 정수일 때

이다. 따라서 인 성질을 가지므로

이다. 그러므로

와 같이 표현할 수 있다. 따라서 에 대응하는 급수해   은 다음과 같다.

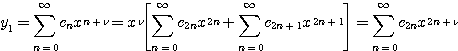
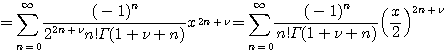
로 된다.   이면 이 급수는 구간 에서 수렴한다.

일반적으로 위 급수를 로 표시한다. 즉

(4.32)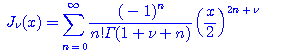                                  

(II) 인 경우

   식 (4.31)에서 순환관계식

을 얻는다. 그런데 이것은   인 경우에서 를 로 대치한 것과 같으므로 인 경우에서와 같은 방법으로

(4.33)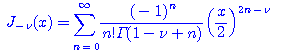                                                                         

을 얻는다. 함수 와 를 각각 위수가 와 인 제 1종의 Bessel 함수(Bessel function of the first kind)라고 한다.

의 값에 따라 식 (4.33)의 는 의 음의 멱승도 포함할 수 있다.

       Bessel 함수의 몇가지 유용한 성질을 살펴보자. 우선 이 양의 정수이면 는 1차종속임은 다음 정리에서

알 수 있다.

정리 4.3.1     이 양의 정수이면

증명

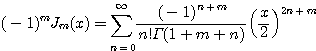
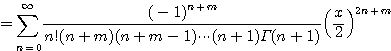
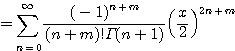
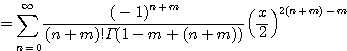
정리 4.3.2     이 양의 정수이면

증명

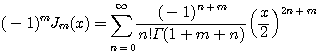
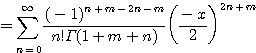
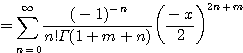
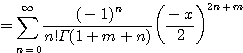
     정리 4.3.2에서 이 짝수이면 는 우함수(even function), 이 홀수이면 는 기함수(odd function)임을

알 수 있다.

     Bessel 방정식 (4.30)의 일반해는 의 값에 따라 경우가 나누어질 것이다.

제 1.4.2절에서 언급하였듯이 이면 식 (4.32)과 (4.33)는 같다. 즉 두번째 해는 다시 구해야 할 것이다.

  이면 이므로 서로 다른 실근이지만 가 양의 정수인지 아닌지에 따라

달라질 것이다.

       제 1.4.2절의 경우 I 에서와 같이 가 양의 정수가 아니면 와 는 Bessel 방정식 (4.30)의1차독립인

해이고 따라서 일반해는 일 것이다.

      제 1.4.2절의 경우 II 에서와 같이 가 양의 정수일 때는 둘째 급수해를 구해야 할 것이다. 이 경우 즉 가

양의 정수인 경우도 두 가지 가능성을 생각할 수 있다. 인 경우와   인 경우가 생각되어진다.

인 경우일 때는 는 의 상수배임을 정리 4.3.1로부터 알 수 있으므로   와 는 1차종속인

해이다.

     한편 의 경우에 있어서는 와 는 1차독립이다. 다시 말하면 Bessel 방정식 (4.30)의 일반해는

이면                                          

(4.34)                                                           

이다.

예제 4.3.1    의 일반해를 구하라.

풀이   인 즉 인 Bessel 방정식이므로 이 미분방정식의 일반해는

예제 4.3.2    의 일반해를 구하라.

풀이    인 즉   인 Bessel 방정식이므로 이 미분방정식의 일반해는

      이제 가 정수인 경우의 해를 구하기 위하여 경수변화법을 사용하자. 즉 라 하면

이므로 Bessel 방정식 (4.30)에 대입하면

(4.35)                      

를 얻는다. 더욱이 가 식 (4.30)의 해이므로

가 되어 식 (4.35)로부터

(4.36)                                                

을 얻는다.   로 식 (4.36)의 양변을 나누면

(4.37)                                                 

가 된다.   라 하면 식 (4.37)은

(4.38)                                               

의 변수분리형 미분방정식이 되어 양변을   에 관하여 적분하면

이 되어    이므로

이다. 따라서     

그러므로 에 1차독립인 다른 한해는

이다. 한편

(4.39)                                    

를 위수가 인 제 2종의 Bessel 함수(Bessel function of the second kind of order $\nu$ --> ) 또는

$\nu$ --> 차 Neumann 함수(Neumann's function)이라 한다.

       이상의 내용으로부터 Bessel 방정식 (4.30)의 일반해는 다음과 같다.

정리 4.3.3   Bessel 방정식 (4.30)의 일반해는

(1)   ( 은 정수)이면  

(2)   ( 은 정수)이면  

       한편   가 정수인 경우 제 1.4.2절의 경우 III 을 이용하기 위하여

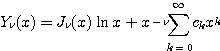
라 하면

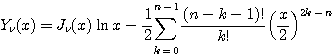
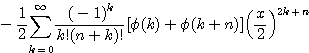
이다. 단 이다.

      특히 이면

이고 더욱이 가 이 아니고 양의 정수도 아니면

(4.40)                                            

가 된다.   가 정수가 아니면   와 는 Bessel 방정식 (4.30)의 1차독립인 해이다. 따라서 식 (4.30)의 일반해의

다른 형식은   이면 이다.

        ( 은 정수)일때 식 (4.40)은 부정형   이 된다. 그러나 법칙에 의하면 를 구할 수 있다.

더구나 함수   와 는 Bessel 미분방정식 의 1차독립인 해이다.

따라서 우리는 다음의 사실을 알 수 있다.

정리 4.3.4   Bessel 방정식 (4.30)의 일반해는 임의의 값 에 대하여

(4.41)                                                 

예제 4.3.3   의 일반해를 구하라.

풀이     즉   이므로 식 (4.41)로부터 일반해는

       Bessel 방정식 (4.30)에서 를 로 대치하여 보자.

연쇄법칙을 사용하여

을 식 (4.30)에 대입하면

즉,

                                                       다시 말하면

(4.42)                                                

라는 다른 형태의 Bessel 방정식을 얻을 수 있다. 이것을 매개변수 Bessel 방정식 (parametric Bessel equation)이라 한다.

식 (4.42)의 일반해는

(4.43)                                                  

이다.

예제 4.3.4    의 일반해를 구하라.

풀이  주어진 방정식은 인 매개변수 Bessel 방정식이므로 식 (4.43)에 의하여 일반해는

예제 4.3.5    의 일반해를 구하라.

풀이  주어진 미분방정식의 양변을 9로 나누면

이므로 인 매개변수 Bessel 방정식이다. 일반해는 식 (4.43)에 의하여

                                                                      연습문제 1.4.3.1

1. 다음 미분방정식의 일반해를 구하라.

(1)                                                    (답: )

(2)                                                                     (답: )

(3)                                                       (답: )

(4)                                                                   (답: )

2. 다음 공식을 유도하라.     

(1)  

(2)  

(3)  

(4)  

(5)  

1.4.3.2 Legendre 방정식의 급수해

        Legendre 방정식

(4.44)                                                

의 급수해를 구해보자.

        는 Legendre 방정식 (4.44)의 정상점이므로   을 해라고 가정한다. 따라서

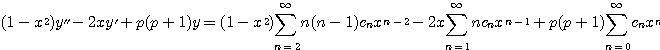
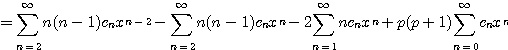
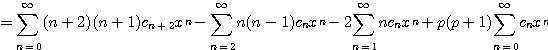
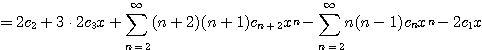
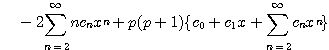
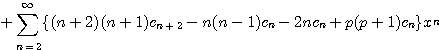
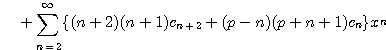
이므로              

즉                                                       

(4.45)                                               

식 (4.45)를 반복하면

따라서 Legendre 방정식 (4.44)의 급수해는 임의의 상수 $c_0, \; c_1$ --> 에 대하여

(4.46)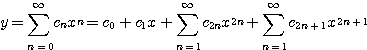                                

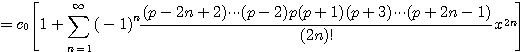
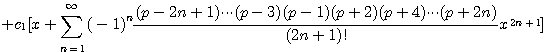
(4.47)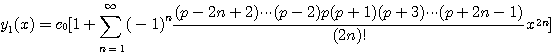                           

(4.48)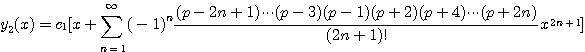                          

이라 하면 는 우함수이고,   는 기함수이므로 는 1차독립이다.

즉 식 (4.46)은 Legendre 방정식 (4.44)의 일반해이다.

식 (4.46)을 살펴보면 만일 가 짝수이면 는 항까지의 유한항으로 끝나 유한급수이고,

는 무한급수임을 알 수 있다.

      같은 이유로 가 홀수이면 가 항까지의 유한항으로 끝나 유한급수이고,

는 무한급수이다. 즉, 가 음이 아닌 정수이면 Legendre 방정식의 차 다항식의 해를 얻는다.

     Legendre 방정식의 해의 상수배는 또한 해이므로 가 양의 짝수 또는 홀수이냐에 따라서 와 에 대한 특수값을

다음과 같이 정하는 것이 표준관례이다.

에 대해서는 에 대해서는

을 택하고,

에 대해서는 에 대해서는

을 택한다.

이들 특수 차 다항식 해를 Legendre 다항식(Legendre polynomials)라 하고 로서 표시한다.

    에 대한 급수와 의 선택을 통하여 다음 여러가지 Legendre 다항식을 구해보면

(4.49)                       

임을 알 수 있다.

는 차례로  다음 미분방정식의 특수해이다.

정리 4.3.5     : Legendre 다항식은 아래의 성질을 만족한다.

(1)  

(2)  

(3)  

(4)  

(5)  

      정리 4.3.5의 (1)로부터 가 짝수면 는 우함수이고, 가 홀수면 는 기함수임을 알 수 있다.

또한 Legendre 다항식 는 다음 정리로서 주어진다.

정리 4.3.6   Rodrigues 공식

증명    라 두면

이므로

이다. 이 식을 에 관하여 미분하면

이고 다시 에 관하여 번 미분하면, 이라고 하면

이다. 이 식에서 라고 하면

이고 이 방정식은 차 Legendre 방정식이다. 따라서 는 Legendre 방정식의 해이다.                                                 

한편

이므로 는 차 다항식이고, 또한 Legendre 방정식은 다항식 형태의 해를 가지므로 는 의 상수배이다.

따라서

이므로

임을 알 수 있다.

한편 정리 4.3.5에서 이므로   이다. 따라서

          이제 Legendre 다항식에 대한 성질을 알아보자.

정리 4.3.7       

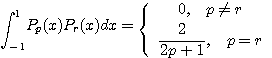
증명   Rodrigues 공식에 의하여

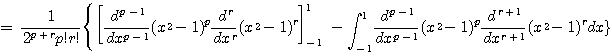
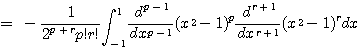
계속해서 부분적분을 시행하면  

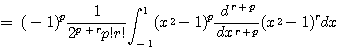
(i) 인 경우 : 만약   이라 하면   이므로

즉, 이면 이다.

이라 하면 역시 같은 이유로  

(ii) 인 경우 :

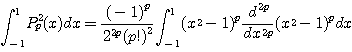
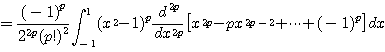
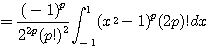
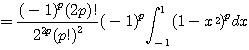
정리 4.3.8    를 에 관한 차 다항식이라 하자. 그러면 일때

증명    는 에 관한 차 다항식이므로 적당한 상수 에 대하여 는 차 다항식이고,

는 차 다항식으로 적당한 상수 에 대하여 는 차 다항식이다.

이러한 방법을 반복 시행하면 적당한 상수들 에 대하여

는 어떤 상수 되게 할 수 있다.

     한편 식 (4.49)에서 이므로 라 쓸 수 있고 따라서

즉

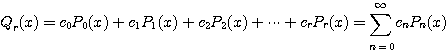
이다. 그러므로

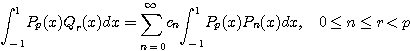
이므로 정리 4.3.7에 의하면 이다. 따라서

정리 4.3.9  구간 에서 정의되는 함수 는 Legendre 다항식의 급수로 전개할 수 있다. 즉

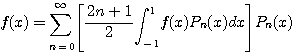
증명    

이므로 정리 4.3.7에 의하여

즉

이다. 그러므로

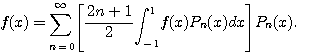
예제 4.3.6      을 Legendre 다항식의 급수로 나타내어라.

풀이   라 하자.

여기서 이고 식 (4.49)로부터

이므로 을 대입하여 을 구하면 된다.

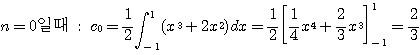
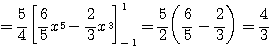
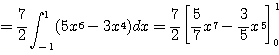
따라서

       이제 Potential 이론에서 중요하게 사용되는 사실을 알아보자.

정리 4.3.10   

증명   이항정리에 의하여

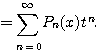
     정리 4.3.10 이 나타내는 것은 Legendre 다항식 는 을 의 멱으로 전개할 경우 의 계수와 같다는

것이다. 이때 식 을 Legendre 다항식에 대한 모함수(generating function)이라고 한다.

                                                                           연습문제 1.4.3.2

1. 다음의 Legendre 다항식을 구하라.

(1)                                                                                

 (답: )

(2)                                                                               

 (답: )

(3)                                                                                

 (답: )

(4)                                                                                

 (답: )

(5)                                                                                

 (답: )

(6)                                                                                

 (답: )

2. 다음 함수를 Legendre 다항식으로 전개하라.

(1)                                                                             

 (답: )

(2)                                                                     

 (답: )

(3)                                                   

 (답: )

3. 임을 보여라.

4. 다음 미분방정식의 일반해를 구하라.    

(1)                                                     

 (답: 인 Legendre 다항식)

(2)                                       

 (답: 인 Legendre 다항식 대신 대입)