1.3.4 상수계수 비동차 선형미분방정식

        앞에서 언급한 바와 같이 상수계수 비동차선형미분방정식의 일반형은

(3.21)                                        

이며 식 (3.21)의 일반해는

(3.22)                                         

의 일반해 와 식 (3.21)의 특수해 의 합이다. 즉 식 (3.21)의 일반해는

이다. 다시 말하면 식 (3.22)의 일반해를

이라 하면 식 (3.21)의 일반해는

이다.

예제 3.4.1

   를 특수해로 갖는 미분방정식 의 일반해를 구하라.

풀이  주어진 미분방정식의 동차미분방정식 의 일반해 를 구하자.

        보조방정식 로부터   이므로   이다.

       그러므로 주어진 비동차미분방정식의 일반해는

      위 예제에서 알 수 있듯이 비동차선형미분방정식의 일반해를 구하기 위해서는 특수해를 알아야 한다.

따라서 특수해 구하는 방법에 대하여 알아보자.

1.3.4.1 미정계수법

       하나의 함수를 다른 함수로 변환시키는 연산을 연산자(operator)라 한다. 도함수를 구하는 연산 를 연산자

로 나타내자. 즉   와 같이 표현한다. 이때 연산자 를 미분연산자 (differential operator)라 한다.

미분가능한 함수   와 임의의 상수   에 대하여

가 성립하므로 이 미분연산자는 선형(linear)이다. 미분연산자 $D$ --> 에 대하여

이므로 식 (3.22)는

와 같이 표현할 수 있다. 이때

을   라고 한다.

계수가 상수인 미분연산자 는 인수분해가능하며 의 인수는 또한 교환가능하다.

또한 을 식 (3.22)의 특성방정식(characteristic equation) 또는 보조방정식(auxiliary equation)이라 하고

특성방정식의 해를 특성근(characteristic root) 이라 한다.

      상수계수 미분연산자 는 교환법칙이 성립한다. 예를 들면

그런데   이므로

한편

그러므로  

      하지만, 상수가 아닌 변수계수인 미분연산자 는 교환법칙이 성립하지 않는다. 예를 들면

그런데 로 인수분해되어지지만

한편

그러므로  

       가 적어도   계의 도함수를 갖는 함수라고 하자. 만약

(3.23)                                     

이면 미분연산자 는 를 으로 만든다.

만약 (상수) 이면 로 미분연산자 는 상수를 0으로 만든다. 또한   등으로

(3.24)                 미분연산자  은   인 각 함수를   으로 만든다.

    의 다항식의 경우 의 최고차수를 으로 만드는 연산자를 취하여 으로 만들 수 있다.

제 1.3.3 절에서 보았듯이 의 보조방정식은 이고   는 중복도가   인 근이므로 일반해는

임을 상기하여

(3.25)                미분연산자 은 의 각 함수를 으로 만든다.

     또한 보조방정식 인 경우 복소수근 을 중복도 으로 가질때의 일반해가

이었음을 상기하여

(3.26)                미분연산자 은

                        의 각 함수를 으로 만든다.

      특별히 인 경우를 생각하면, , 임을 쉽게 알 수 있다.

예제 3.4.2   다음 함수를 0으로 만드는 미분연산자를 구하라.

        1.                           2.  

        3.                    4.  

풀이   

1. (3.25)에서 이므로   이므로 로 부터

2. (3.24)에서 이므로 ,  

    (3.26)에서 이므로 로 부터    

3. (3.25)에서 이므로 ,

    (3.24)에서 이므로 ,

    (3.25)에서 이므로 로부터

4. (3.26)에서 이므로

       식 (3.21)을 미분연산자 를 사용하여 나타내면

(3.27)                                                       

비동차 선형미분방정식 (3.21)의 일반해를 구하는 방법을 알아보자.

(1) 먼저 인 경우, 즉 동차 선형미분방정식의 일반해   를 구한다.

(2) 식 (3.21)의 우변 를 으로 만드는 다른 미분연산자 를 구하여 식 (3.27)에 적용시키면

즉, 의 동차 선형미분방정식을 얻을 수 있고, 앞에서 배운대로 의 일반해 를 구한다.

가

                (a) 상수  

                (b) 의 다항식

                (c) 지수함수  

                (d)  

                (e) 의 각 항이 (a), (b), (c), (d)의 유한곱

인 경우에는 를 으로 만드는 미분연산자 를 구할 수 있다.

(3) 비동차방정식의 일반해는 동차방정식의 일반해와 비동차방정식 의 특수해와의 합으로 나타나므로 즉,

이므로 (2)에서 구한 일반해 에서 (1)에서 구한 를 제외한 나머지가 특수해 가 될 것이다. 이 를

식 (3.21)에 대입하여 양변의 계수비교로 구한다.

(4) 비동차선형미분방정식의 일반해는 이다.  

       이와 같이 를 구하는 방법을 미정계수법 (method of undetermined coefficients)이라 한다.

예제 3.4.3    의 일반해를 구하라.

풀이

(1) 의 일반해   를 구하자.

    보조방정식 로부터 이므로

(2) 을 으로 만드는 미분연산자를 찾는다.

     (3.25)에서 이므로  

    그러므로 이다.

    주어진 미분방정식 에   를 적용시키면 가 되어

    동차 미분방정식을 얻게 된다.

    보조방정식 로부터   , 이므로

(3) 를 주어진 미분방정식에 대입하여 를 구한다.

이므로

계수비교에 의해   을 얻을 수 있다.  따라서 이다.

(4) 그러므로 (1), (2), (3)의 결과로부터 주어진 미분방정식의 일반해는

                                          .

예제 3.4.4    의 일반해를 구하라.

풀이

(1) 의 일반해 를 구한다.

    보조방정식   로부터   이므로

(2) 을 으로 만드는 미분연산자 를 구한다.

    (3.26)에서 이므로 이다.

    주어진 미분방정식 에 를 적용시켜 의 동차방정식을 얻는다.

    보조방정식 의 근을 구하면 이므로

(3) 를 주어진 미분방정식에 대입하여 를 구한다.

     이므로

계수비교하면  

의 연립방정식을 얻고, 연립방정식으로부터   을 구할 수 있다.  따라서  

(4) 그러므로 (1), (2), (3)의 결과로부터 주어진 미분방정식의 일반해는

예제 3.4.5   다음 초기치 문제의 해를 구하여라.

풀이

(1) 의 일반해 를 구하자.

   보조방정식 로부터 이므로   .

(2) 를 으로 만드는 미분연산자 는 이므로 주어진 미분방정식

    에 를 적용시켜 의 동차방정식을 얻는다.

    보조방정식 로부터   이므로

(3) 에서 미정계수를 구하자

이므로

계수비교에 의하여    

따라서    

(4) 주어진 미분방정식의 일반해는

(5) 초기치 조건을 만족하는  

그러므로    

조건을 대입하기 위해 우선   을 구하자.

따라서 . 그러므로 구하는 해는

                                                       연습문제 1.3.4.1

1. 다음 함수를 으로 만드는 미분연산자를 구하라.

(1)                                                         (답: )

(2)                                              (답: )

(3)                                                             (답: )  

(4)                                                        (답: )

(5)                                                       (답: )

(6)                                                    (답: )

(7)                                                (답: )

(8)                                            (답: )   

(9)                                              (답: )

(10)                               (답: )

2. 다음 미분방정식의 일반해를 미정계수법을 사용하여 구하라.

(1)                  

 (답: )

(2)                                                                                     

 (답: )

(3)                                                                         

 (답: )

(4)                                                                        

 (답:   )

(5)                                               

 (답: )

(6)                                                                   

 (답: )

3. 다음 초기치 문제를 풀어라.

(1)                                  

 (답: )

(2)                                        

 (답:   )

 1.3.4.2 경수변환법

       계 비동차 상수계수선형미분방정식의 일반형

(3.28)                                      

에 대한 동차방정식

(3.29)                                       

의 일반해

에 대하여 상수들   을 함수   로 대치하여 만들어진 함수

가 식 (3.28)의 특수해가 되도록    을 결정하는 방법을 경수변화법(variation of parameter)이라 한다.

    제 1.2.6절에서 1계 선형미분방정식

(3.30)                                                                 

의 일반해는

(3.31)                                                 

임을 증명한 바 있다. 여기서 와 는 임의의 구간 에서 연속이다.

그런데 식 (3.31)의 형태는   이며

(3.32)                                                                  

는 의 일반해이며

(3.33)                                                           

는 식 (3.30)의 특수해이다. 여기서 경수변화법을 사용하여 특수해 (3.33)을 구해보자.

       제 1.2장에서

가   의 해가 됨을  증명하였다. 이 미분방정식은 선형이므로 일반해는 이다.

경수변화법이란   을 함수 로 대치한 후 가 특수해가 되도록 을 구하는 것이므로 를 식 (3.30)에 대입하면

즉

에서 으로 묶으면  

이므로

이고 이 미분방정식을 변수분리형으로 변형하면

이므로

이다. 그러므로

즉, 식 (3.33)을 얻는다. 이 방법을 2계 선형 미분방정식

(3.34)                                                         

에 적용하자.   라고 가정하고 양변을    로 나누어 표준형

(3.35)                                                          

으로 고친다. 여기서 와 는 임의의 구간 에서 연속이라 가정한다. 동차방정식

(3.36)                                                            

의 1차독립인 해를   라고 하자. 즉   이다.

경수변화법을 사용해서 즉 를   로 대치한   가 식 (3.35)의 특수 해가 되도록 를 구하면 된다.

(3.37)                                                           

더욱이 가

(3.38)                                                                    

을 만족하는 함수라고 하면 식 (3.37)은

(3.39)                                                                    

가 되고

이다. 따라서 이것을 식 (3.35)에 대입하면

이고   이므로 는

(3.40)                                                         

를 만족해야 한다. 즉 (3.38), (3.40)을 모두 만족하는 함수를 구하면 된다:           

(3.41)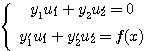                                                          

즉

(3.42)                                                       

이것은 에 대한 연립방정식이므로 Cramer공식에 의해

이다. 여기서

            ,        ,           

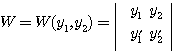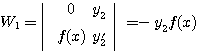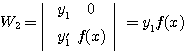
이고, 는 1차독립이므로 임은 분명하다. 따라서

이고, 특수해   를 구할 수 있다.

예제 3.4.6     의 일반해를 구하라.

 풀이    의 보조방정식 로 부터 이므로

                                                                     .

경수변화법을 이용하여 특수해를 구하기 위해

라고 둔다. 여기서 이므로

그러므로

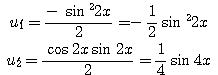
따라서

이다. 그러므로 특수해는

따라서 일반해는

예제 3.4.7    의 일반해를 구하라.

풀이    의 보조방정식   로 부터

이다. 이제 라고 하면

그러므로

따라서

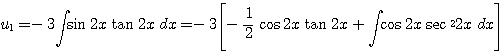
그러므로

따라서 일반해는

        의 부정적분을 구할 때 적분상수는 가져오지 않아도 된다. 그 이유는 아래에서 확인될 수 있듯이 적분상수

를 첨가하더라도 같은 결과를 얻기 때문이다.                             

이제 특수해를 구하는 한 방법인 경수변화법을 표준형 계 비동차선형미분방정식

(3.43)                                    

으로 일반화시켜보자.

이 인 동차선형미분방정식의 일반해라고 하면

로 두고 주어진 비동차선형미분방정식 (3.43)에 대입하여 을 구하면 된다.

를 얻게되며 2계 비동차선형미분방정식의 경우와 같이

의 조건을 두게 되면

이 성립된다. 또한   를 미분하여

을 구할 수 있다. 가 만족할 두번째 조건

으로부터

을 얻게 된다. 이 과정을 반복하여

(3.44)                                      

(3.45)                                      

와

(3.46)                        

을 유도해낼 수 있다.

        식 (3.45), (3.46)을 식 (3.43)에 대입하여   이 동차방정식의 해임을 이용하여                                                        

(3.47)           

를 얻게 된다.

      식 (3.44)와 식 (3.47)로부터 을 미지수로 하는 다음 선형방정식을 얻게 된다.

(3.48)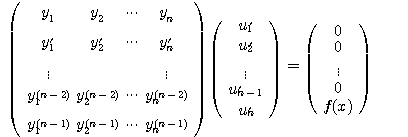                                     

이 식으로부터

(3.49)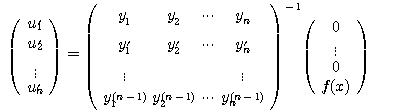                                    

을 얻는다.

     알려진   및 주어진 를 식 (3.49)에 대입하여 를 구한 뒤 이들을 각각 적분하여

을 구하여

을 찾는다.

        를 구하는 또 다른 방법을 생각해보자.

         즉, 의 Wronskian이고 는 Wronskian 의 번째열의 성분을

로 대치한 행렬식이라 하자. 즉,

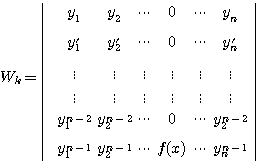
그러면

이 된다.  따라서 주어진 비동차선형미분방정식 (3.41)의 특수해는

이다. 그러므로 일반해는

미정계수법이 가 제 1.3.4절에서 제시한 특수한 함수형태에 제한되는 것과 달리 경수변화법은 제한 받지 않는

잇점이 있다.

예제 3.4.8      의 일반해를 구하라.

풀이    의 보조방정식   로 부터

이고   라 하면   라 두고   를 구해야 한다.

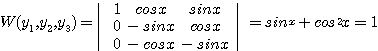
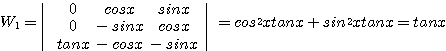
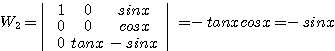
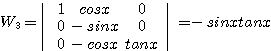
이므로  

따라서

그러므로 일반해는

                                                               연습문제 1.3.4.2

1. 다음 미분방정식의 일반해를 경수변화법을 사용하여 구하라.

(1)                                      

 (답: )

(2)                                  

 (답:  

(3)                                    

 (답: )

(4)              

 (답: )

(5)                     

 (답: )

(6)                           

 (답: )

2. 다음 초기치 문제를 풀어라.

(1)                    

 (답: )

(2)          

 (답: )

(3)                     

 (답: