1.2.3 동차비분방정식 1.2.4 완전미분방정식
1.2.3 동차비분방정식
동차미분방정식을 정의하기에 앞서 우선 동차함수에 대하여 살펴보자.
정의 2.3.1 임의의
![]() 에 대하여
에 대하여 ![]() 가 성립할 때
가 성립할 때 ![]() 를
를 ![]() 차동차함수(homogeneous function)라 한다.
차동차함수(homogeneous function)라 한다.
동차함수란 각 항의 차수의 합이 같음을 의미한다.
예제 2.3.1 다음의 주어진 함수가 동차함수인지 아닌지를 판별하라.
(1) ![]()
(2) ![]()
(3) ![]()
풀이
(1) ![]()
![]()
![]()
![]()
![]() 는 3차 동차함수이다.
는 3차 동차함수이다.
(2) ![]()
![]()
![]()
그러므로 ![]() 는
는![]() 의 차수가 1 이므로 동차함수가 될 수 없다.
의 차수가 1 이므로 동차함수가 될 수 없다.
(3) ![]()
![]()
![]()
![]()
![]() 는 1차 동차함수이다.
는 1차 동차함수이다.
미분방정식
(2.4) ![]()
에서 ![]() 와
와![]() 가 같은 차수의 동차함수일 때 (2.4)를 동차미분방정식 (homogeneous
differential equation)
가 같은 차수의 동차함수일 때 (2.4)를 동차미분방정식 (homogeneous
differential equation)
이라 한다.
동차미분방정식은 치환에 의하여 항상 변수분리형 미분방정식으로 변형된다.
치환 ![]() 혹은
혹은 ![]() 를 이용하여 미분방정식 (2.4)는 변수분리형 미분방정식으로 변형될 수 있다.
를 이용하여 미분방정식 (2.4)는 변수분리형 미분방정식으로 변형될 수 있다.
여기서![]() 와
와 ![]() 는 각각
는 각각![]() 에 의존하는 새로운 종속변수이다.
에 의존하는 새로운 종속변수이다.
만일 치환![]() 를 적용하여 양변을
를 적용하여 양변을 ![]() 에 대하여 미분하면
에 대하여 미분하면
![]()
미분방정식 (2.4)는
![]()
으로 된다.![]() 이
이 ![]() 차 동차함수이면
차 동차함수이면
![]()
이므로 다음과 같이 변수분리형 미분방정식으로 변형된다.
![]()
치환 ![]() 를 실시하면
를 실시하면
![]()
을 얻게된다.
여기서 소개된 두 가지 치환중에서 어떤 것을 선택해야 하는가 하는 기준은 다음과 같이 설정해 볼 수 있다.
![]() 에 비하여
에 비하여 ![]() 식이 더 복잡하면
식이 더 복잡하면 ![]() 치환을 사용하는 것이 일반적으로 보다 간단한 식을 얻을 수 있다.
치환을 사용하는 것이 일반적으로 보다 간단한 식을 얻을 수 있다.
역으로 ![]() 에 비하여
에 비하여 ![]() 식이 더 복잡하면
식이 더 복잡하면 ![]() 치환을 적용하는 것이 바람직하다.
치환을 적용하는 것이 바람직하다.
그러나 한가지 치환을 실시했을때 적분불가능한 식을 얻게 되면 다른 치환으로 시도해 볼 수 있다.
예제 2.3.2 ![]() 을 풀어라.
을 풀어라.
풀이 ![]() 이 2차동차함수이므로 치환
이 2차동차함수이므로 치환 ![]() 를 실시하면
를 실시하면
![]()
변수분리형 미분방정식으로 변형하면
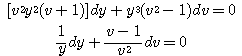
을 얻는다. 위의 식을 ![]() 에 대하여 각각 적분하면
에 대하여 각각 적분하면
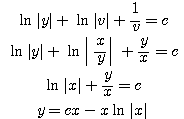
를 얻게 된다.
예제 2.3.3 ![]() 을 풀어라.
을 풀어라.
풀이 ![]() 가 3차동차함수이며
가 3차동차함수이며 ![]() 이
이 ![]() 보다 간단하므로 치환
보다 간단하므로 치환 ![]() 를 적용하면
를 적용하면
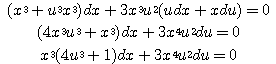
을 얻게 된다. 위 식을 변수분리하여 적분하면
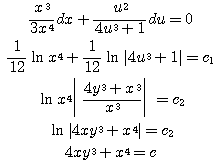
를 얻는다.
연습문제 1.2.3
1. 다음 함수들이 동차함수인지 아닌지를 판단하라. 동차함수이면 차수를 결정하라.
(1) ![]() (답: 동차함수, 차수=4)
(답: 동차함수, 차수=4)
(2) ![]() (답: 비동차함수)
(답: 비동차함수)
(3) ![]() (답: 동차함수, 차수=0)
(답: 동차함수, 차수=0)
(4) ![]() (답: 비동차함수)
(답: 비동차함수)
(5) ![]() (답: 동차함수, 차수=0)
(답: 동차함수, 차수=0)
(6) ![]() (답: 동차함수, 차수=-2)
(답: 동차함수, 차수=-2)
2. 다음 동차방정식을 적당한 치환에 의하여 해를 구하라.
(1) ![]() (답:
(답:
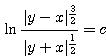 )
)
(2) ![]() (답:
(답: ![]() )
)
(3) ![]() (답:
(답:
![]() )
)
(4) ![]() (답:
(답:
![]() )
)
3. 다음 초기치 문제의 해를 구하라.
(1) ![]() (답:
(답:
![]() )
)
(2) ![]() (답:
(답:
![]() )
)
(3) ![]() (답:
(답:
![]() )
)
4. 동차방정식![]() 는 치환
는 치환![]() 에 의하여 변수분리형미분방정식으로
에 의하여 변수분리형미분방정식으로
변환시켜보라.
5. 동차방정식 ![]() 는
는 ![]() 로 변형될 수 있음을 보여라.
로 변형될 수 있음을 보여라.
1.2.4 완전미분방정식
![]() 공간의 영역
공간의 영역 ![]() 에서 정의된
에서 정의된 ![]() 의 편도함수
의 편도함수 ![]() 가 연속일 때,
가 연속일 때, ![]() 의 전미분은
의 전미분은
(2.5) ![]()
로 정의되어진다.
만약 ![]() 가 어떤 영역
가 어떤 영역 ![]() 에서
에서![]() 이면 식 (2.5)로 부터
이면 식 (2.5)로 부터
![]()
가 된다.
이로부터 주어진 방정식
(2.6) ![]()
가 ![]() 을 만족하는
을 만족하는 ![]() 가 존재한다면 방정식 (2.6)의 해는
가 존재한다면 방정식 (2.6)의 해는![]() 가 될것이다.
가 될것이다.
정의 2.4.1 어떤
함수 ![]() 에 대하여
에 대하여
![]()
가 성립되면 미분방정식 ![]() 를 완전미분방정식(exact differential equation)이라
한다.
를 완전미분방정식(exact differential equation)이라
한다.
그러면 우리는 아래의 두 가지 문제를 생각해 볼 수 있다.
(1) ![]() 가 완전미분방정식인가?
가 완전미분방정식인가?
(즉 ![]() 를 만족하는
를 만족하는 ![]() 가 존재하는가?)
가 존재하는가?)
(2) 만약 주어진 방정식이 완전미분방정식이라면 ![]() 를 어떻게 구할 것인가?
를 어떻게 구할 것인가?
다음 정리에서 물음 (1)에 대한 해답을 찾아보기로 하자.
정리 2.4.1 ![]() 가 영역
가 영역![]() 에서 연속인 1계 편도함수를
에서 연속인 1계 편도함수를
가진다고 가정했을 때, ![]() 이 완전미분방정식이 될 필요충분조건은
이 완전미분방정식이 될 필요충분조건은
![]()
증명
(i) ![]() 가 완전미분방정식이면
가 완전미분방정식이면
![]()
를 만족하는![]() 가 존재한다.
가 존재한다.
그러므로 영역 ![]() 에서
에서 ![]() 가 성립된다.
가 성립된다.
![]()
여기서 ![]() 인 것은 함수
인 것은 함수 ![]() 이 연속인 1계
편도함수를 가지므로 가능하다.
이 연속인 1계
편도함수를 가지므로 가능하다.
(ii) ![]() 가 완전미분방정식이 되기 위해서는
가 완전미분방정식이 되기 위해서는
![]()
를 만족하는 ![]() 가 존재하여야 한다. 즉,
가 존재하여야 한다. 즉,
![]()
를 만족하여야 하므로 우선, ![]() 의 양변을
의 양변을 ![]() 에 대하여 적분하면
에 대하여 적분하면
![]()
를 얻게 된다. 즉
(2.7) ![]()
를 얻게 된다. 여기서 ![]() 는
는 ![]() 에 대하여 적분하였을 때 적분상수이다.
에 대하여 적분하였을 때 적분상수이다.
위 식을 ![]() 에 대하여 편미분을 취하면
에 대하여 편미분을 취하면
![]()
(2.8) ![]()
우변의 식 ![]() 는
는
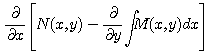
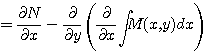
![]()
이므로 ![]() 와 무관한
와 무관한 ![]() 만의 함수이다.
만의 함수이다.
그러므로 ![]() 를
를 ![]() 에 관하여 적분하여
에 관하여 적분하여 ![]() 를 구할 수 있다.
를 구할 수 있다.
위의 증명 (ii)는 ![]() 가 완전미분방정식일때 방정식의
해
가 완전미분방정식일때 방정식의
해 ![]() 를
를
풀이하는 과정을 함께 보여주고 있다. 위의 증명에서는 ![]() 에서 시작하였지만
에서 시작하였지만 ![]()
를 이용하여 ![]() 를 구하여도 같은 결과를 얻을 수 있을 것이다. 이 과정에서 식 (2.7), (2.8)은
를 구하여도 같은 결과를 얻을 수 있을 것이다. 이 과정에서 식 (2.7), (2.8)은
(2.9) ![]()
(2.10) ![]()
로 각각 대치될 수 있을 것이다.
예제 2.4.1 ![]() 가 완전미분방정식임을 보이고
가 완전미분방정식임을 보이고
그 해를 구하라.
풀이
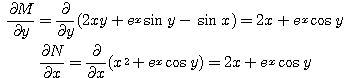
이므로 정리 2.4.1에 의하여 주어진 미분방정식은 완전미분방정식이다.
![]() 보다
보다 ![]() 가 더 간단하므로
가 더 간단하므로
![]()
라 두자. 정리 2.4.1 (ii)의 과정을 따르면
![]()
를 얻는다.
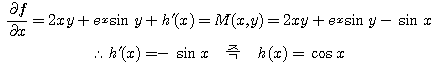
를 얻는다. 따라서 해집합은
![]()
예제 2.4.2 다음 초기치 문제를 풀어라.
![]()
풀이
![]()
이므로 주어진 미분방정식은 완전미분방정식이다.
![]()
이므로 적당한 ![]() 에 대하여
에 대하여
![]()
를 만족한다.
![]()
이 성립해야 하므로
![]()
![]()
따라서 미분방정식의 해집합은
![]()
![]() 을 위 식에 대입하면
을 위 식에 대입하면
![]()
따라서 주어진 초기치 문제의 해는
![]()
연습문제 1.2.4
1. 다음 미분방정식이 완전미분방정식인지를 판단하고 완전미분방정식일 경우 그 해를 구하라.
(1) ![]()
(답: ![]() )
)
(2) ![]()
(답: ![]() )
)
(3) ![]()
(답: ![]() )
)
(4) ![]()
(답: ![]() )
)
(5) ![]()
(답: ![]() )
)
2. 다음 초기치문제의 해를 구하라.
(1) ![]()
(답: ![]() )
)
(2) ![]()
(답: ![]() )
)
(3) ![]()
(답: ![]() )
)
(4) ![]()
(답: ![]() )
)
3. 다음 미분방정식이 완전미분방정식이 될 수 있도록 미지수 ![]() 를 정하라.
를 정하라.
(1) ![]() (답:
(답: ![]() )
)
(2) ![]() (답:
(답: ![]() )
)
(3) ![]() (답:
(답: ![]() )
)
4. 다음 미분방정식이 완전미분방정식이 될 수 있도록 ![]() 를 결정하라.
를 결정하라.
![]()
(답: ![]() 단,
단,
![]() 는 임의의
는 임의의 ![]() 에 대한 함수)
에 대한 함수)
5. 다음 미분방정식이 완전미분방정식이 될 수 있도록 ![]() 를 결정하라.
를 결정하라.
![]()
(답:![]() 단,
단,
![]() 는 임의의
는 임의의 ![]() 에 대한 함수)
에 대한 함수)