Least-squares degree reduction of Bezier type surfacesby Byung-Gook Lee, Applied MathematicsNURBS form recently has become the most widely accepted neutral form for free form curves and surfaces in product model exchange between CAD-systems. In the international standard STEP(Standard for the Exchange of Product Model Data), the NURBS is the only representation for free form curves and surfaces. Therefore, in order to exchange the product data between CAD-systems, other types of curves and surfaces must be converted to B-spline or Bezier curves and surfaces. Hence, efficient algorithms for these conversions are highly desired. Degree reduction of a Bezier surface is a process in which one Bezier polynomial is approximated by another of lower degree. In practice, most computer systems are designed to process curves of degrees less than or equal to a fixed maximum degree. Given a Bezier surface of a degree higher than the maximum that the system can deal with, we must replace it by a curve of lower degree. This often occurs when trying to interface programs from two different computer systems. The process of degree reduction has been used in the fairing of curves and surfaces. In this work we investigate the problem of reducing the degree of Bezier type surfaces (tensor product Bezier surfaces, Bezier triangles). The computations are carry out by minimizing the L2-norm between the two surfaces. We consider the degree reduction of Bezier surfaces as solving the inconsistent linear system. We will use the least-squares method for solving the system by help of "Moore-Penrose inverse" in the statistics. Tensor Product Bezier Surface 1.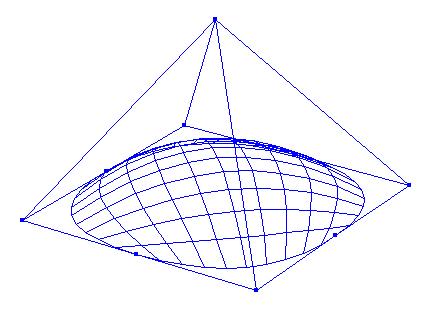 The 3x3 tensor product Bezier polygon vertices are (0 0 1) (1 -1 1) (2 0 1) (-1 1 1) (1 1 3) (3 1 1) (0 2 1) (1 3 1) (2 2 1) Degree Elevation (r=1)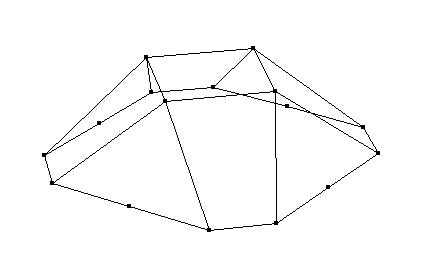 Degree Elevation (r=2)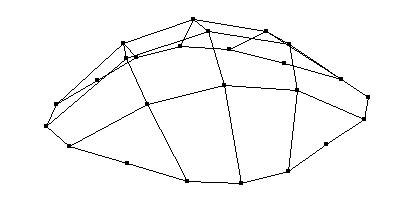 Repeated Degree Elevation (r) Tensor Product Bezier Surface 2.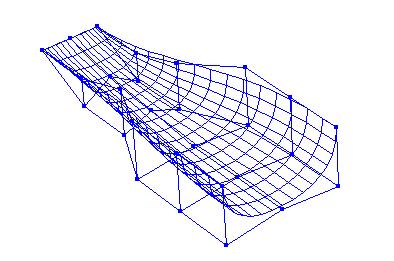 The 5x5 tensor product Bezier polygon vertices are (0 1 1) (1 1 1) (2 1 1) (3 1.5 0.8) (4 1.5 0.5) (5 1.5 0.5) (0 1 0) (1 1 0) (2 1 0) (3 1.5 0) (4 1.5 0) (5 1.5 0.5) (0 2 0.1) (1 2 0.1) (2 2 0.1) (3 2 0.2) (4 2 0.3) (5 2 0.5) (0 3 0) (1 3 0) (2 3 0) (3 2.5 0) (4 2.5 0) (5 2.5 0.5) (0 3 1) (1 3 1) (2 3 1) (3 2.5 0.8) (4 2.5 0.5) (5 2.5 0.5) Repeated Degree Elevation (r)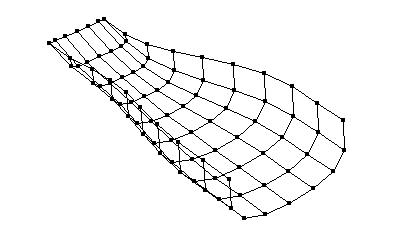 Degree Reduction (r=1)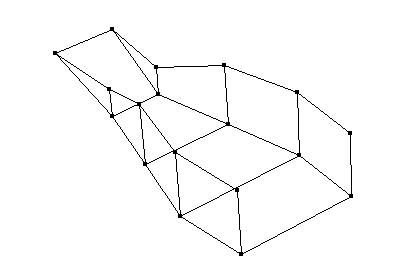 Tensor product Bezier surface after degree reduction (r=1)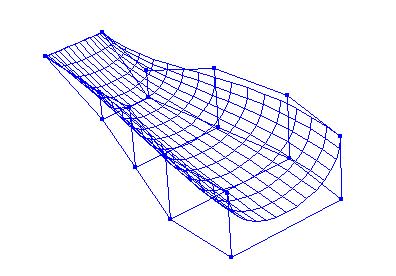 Bezier Triangles 1.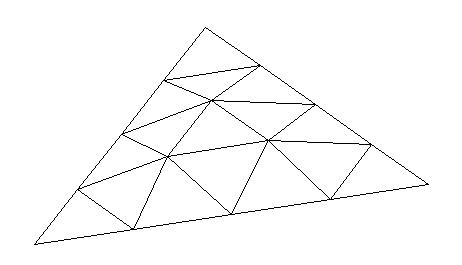 The control net consists of vertices (0 0 0) (1 0 0) (1 1 0) (2 0 0) (2 1 1) (2 2 0) (3 0 0) (3 1 1) (3 2 1) (3 3 0) (4 0 0) (4 1 0) (4 2 0) (4 3 0) (4 4 0) another view point another view point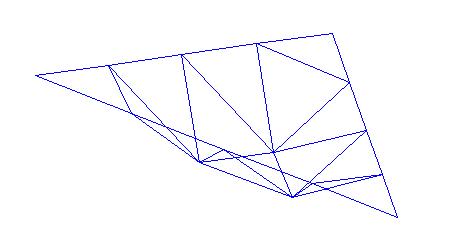 Repeated Degree Elevation (r)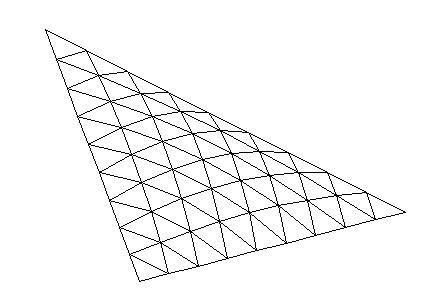 another view point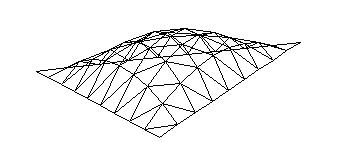 Degree Reduction (r=1)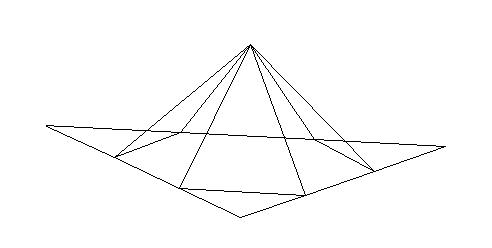 Degree Reduction (r=2) Bezier triangles after degree reduction (r=2) [Last Update: 1998.3.2] `97 Dongseo University Cyber Campus |